2008-2009学年度潍坊市奎文区第二学期七年级期中考试
数学试卷
时间:90分钟 满分:120分
一、选择题(每小题3分,共36分)
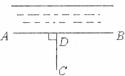
1.如图,点C到直线AB的距离是指( )
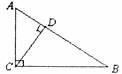
A.AC B.CD C.BC D.BD
2.如果∠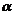 =20°,那么∠
=20°,那么∠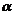 的补角等于( )
的补角等于( )
A.20° B.70° C.110° D.160°
3.直线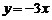 过点(0,0)和点( )
过点(0,0)和点( )
A.(1,-3) B.(1,3) C.(-1,-3) D.(3,-1)
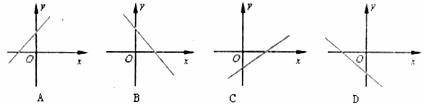
4.一次函数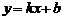 ,当
,当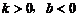 时,它的图象是( )
时,它的图象是( )
5.如图:已知∠1=∠3,那么( )
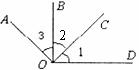
A.∠1=∠2 B.∠2=∠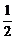 ∠BOD
∠BOD
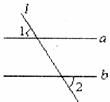
6.如图,直线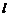 与直线a、b相交,且a∥b,∠1=80°,则∠2的度数为( ).
与直线a、b相交,且a∥b,∠1=80°,则∠2的度数为( ).
A.60° B.80° C.100° D.120°
7.如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )
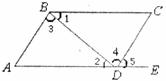
A.∠3=∠4 B.∠A+∠ADC=180° C.∠1=∠2 D.∠A=∠5
8.若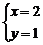 是方程组
是方程组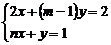 的解,则
的解,则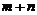 的值是( ).
的值是( ).
A.1 B.2 C.-1 D.-2
9.已知点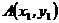 和点
和点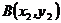 在同一直线
在同一直线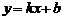 上,且
上,且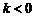 ,若
,若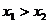 ,则
,则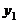 与
与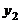 的关系是( ).
的关系是( ).
A.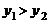 B.
B.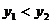
C.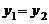 D.
D.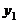 与
与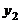 的大小不确定
的大小不确定
10.如图,小明从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
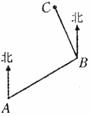
A.右转80° B.左转80° C.右转100° D.左转100°
11.甲、乙二人沿相同的路线由A到B匀速行进,A,B两地间的路程为20km.他们行进的路程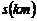 与甲出发后的时间
与甲出发后的时间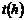 的函数图像如图所示.根据图像信息,下列说法正确的是( )
的函数图像如图所示.根据图像信息,下列说法正确的是( )
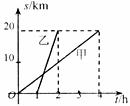
A.甲的速度是4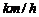 B.乙的速度是10
B.乙的速度是10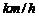
C.乙比甲晚出发1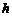 D.甲比乙晚到B地3
D.甲比乙晚到B地3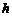
12.直线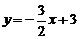 与
与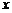 轴、
轴、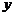 轴所围成的三角形的面积为( ).
轴所围成的三角形的面积为( ).
A.3 B.6 C.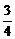 D.
D.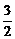
二、填空题(每小题3分,共15分)
13.如图,计划把河AB中的水引到水池C中,可以先作CD⊥AB,垂足为D,然后沿CD开渠,则能使所打开的水渠最短,这种方案的设计根据_______________________________.
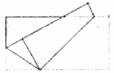
14.如图,将长方形纸片折叠后再展开,折痕的夹角是_______度.
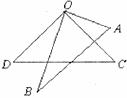
15.如图,将一副三角板替放在一起,使直角的顶点重合于点O,则∠AOD+∠COB的度数为_______度.
16.已知一次函数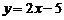 的图象,经过第四象限的一点P
的图象,经过第四象限的一点P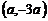 ,则
,则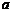 的值是_______.
的值是_______.
17.甲、乙两同学同时解方程组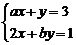 ,甲看错了
,甲看错了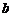 ,求得的解为
,求得的解为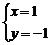 ,乙看错了
,乙看错了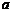 ,求得的解为
,求得的解为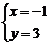 ,则
,则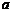 =_______,
=_______,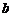 =_______.
=_______.
二、解答题(共69分)
18.解方程组(本小题满分10分)
(1)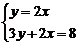
(2)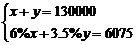
19.(本小题满分9分)
已知一次函数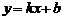 的图象经过点A(2,-4)和点B(6,4),求该函数解析式.
的图象经过点A(2,-4)和点B(6,4),求该函数解析式.
20.(本小题满分10分)
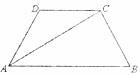
如图,AC平分∠BAD,AB∥CD,能推出∠CAD=∠DCA吗?试说明理由.
21.(本小题满分10分)
已知某山区的平均气温与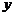 (℃)是该山的海拔高度
(℃)是该山的海拔高度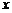 (米)的一次函数.下表列出了一组不同高度时的气温:
(米)的一次函数.下表列出了一组不同高度时的气温:
海拔高度(单位:米)
0
100
200
300
400
…
平均气温(单位:℃)
22
21.5
21
20.5
20
…
(1)求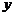 与
与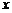 之间的函数关系式.
之间的函数关系式.
(2)若某种植物适宜生长在18℃~20℃(包含18℃,也包含20℃)山区,请问该植物适宜种植在海拔为多少米的山区?
22.(本小题满分10分)
已知:如图,AB,CD,EF三直线相交于一点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,求∠BOG的度数。
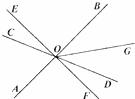
23.(本小题满分10分)
已知,如图,CD⊥AB,GF⊥AB,DE∥BC.试说明∠1=∠2.

24.(本小题满分10分)
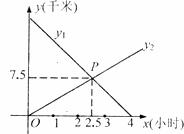
小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,如图所示,图中的线段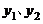 分别表示小东、小明离B地的距离(千米)与所用时间(小时)的关系.
分别表示小东、小明离B地的距离(千米)与所用时间(小时)的关系.
(1)试用文字说明:交点P所表示的实际意义.
(2)试求出A、B两地之间的距离.