2008-2009学年度德州市乐陵第二学期九年级学情调研
数学试卷
说明:本试题满分120分,考试时间120分钟。
第Ⅰ卷(选择题 共24分)
一、选择题:你的数学风采,在于你的合理选择!(本大题共8小题,每小题3分,共24分,在每小题给出的四个选项中有一项是正确的,每小题选对得3分,选错、不选或选出的答案超过一个均记零分)
1.下列调查中,适合用普查方法的是
A.电视机厂要了解一些显像管的使用寿命
B.要了解我市居民的环保意识
C.要了解我市“金丝小枣”的甜度和含水量
D.要了解你校数学教师的年龄状况
2.下列运算中正确的是
A.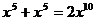 B.
B.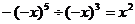
C.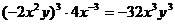 D.
D.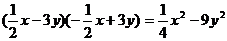
3.二次函数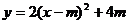 的顶点坐标在直线
的顶点坐标在直线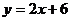 的图像上,则
的图像上,则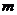 的值等于
的值等于
A.-2 B.-
4.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上方的小三角形。将纸片展开,得到的图形是

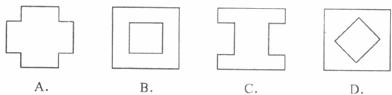
5.不等式组 的解集是
的解集是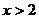 ,则
,则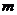 的取值范围是
的取值范围是
A.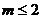 B.
B.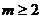 C.
C.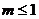 D.
D.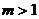
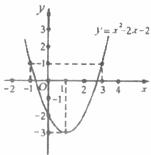
6.已知函数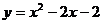 的图像如下图所示,根据其中提供的信息,可求得使
的图像如下图所示,根据其中提供的信息,可求得使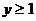 成立的
成立的 的取值范围是
的取值范围是
A.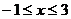 B.
B.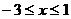
C.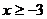 D.
D.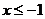 或
或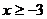
7.如下图,在△ABC中,点Q、P分别是边AC、BC上的点,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,且PR=PS,则下列结论:①AP平分∠BAC;②QP∥AB;③AS=AR;④△BPR≌△QSP,其中正确的有几个
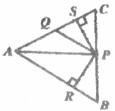
A.1个 B.2个 C.3个 D.4个
8.如下左图,在矩形ABCD中,动点P从点C出发,沿CB运动至点B停止。连结DP,过点A作AE⊥DP,垂足为E,设 ,
,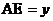 ,如果
,如果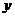 关于
关于 的函数图像如下右图所示,则△ABC的面积为
的函数图像如下右图所示,则△ABC的面积为
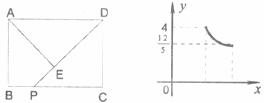
A.4 B.6 C.8 D.12
第Ⅱ卷(非选择题 共96分)
二、填空题:用你敏锐的思维,写出简洁的结果!(本大题共8小题,计32分,只要求填写最后结果,每小题填对得4分)
9.神州7号载人飞船于2008年9月25日21时10分发射升空,历时两天20小时27分35秒。期间航天员进行了舱外行走,在空中的24小时里,神七航天员经历了16个日出日落,飞行了大约68万千米。68万千米用科学记数法表示为_________米(保留三位有效数字)。
10.已知点P(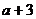 ,
,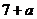 )位于第二象限的角平分线上,则点P的坐标为_________。
)位于第二象限的角平分线上,则点P的坐标为_________。
11.分解因式: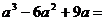 __________________。
__________________。
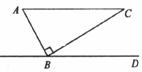
12.如下图,在△ABC中,∠ABC=90°,∠A=65°,BD∥AC,则∠CBD的度数是_________。
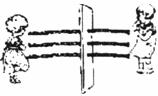
13.如下图,有三条绳子穿过一片木板,姊妹两人分别站在木板的左、右两边,各选该边的一条绳子。若每边每条绳子被选中的机会相等,则两人选到同一条绳子的概率为______。
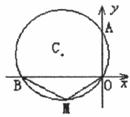
14.如下图,⊙C经过原点且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M 是圆上一点,∠BMO=120°。圆心C的坐标是_________。
15.如下图①是一块瓷砖的图案,用这种瓷砖来铺设地面。如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个。若这样铺成一个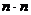 的正方形图案,则其中完整的圆共有_________个(用含
的正方形图案,则其中完整的圆共有_________个(用含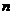 的代数式表示)。
的代数式表示)。

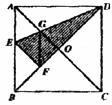
16.如下图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB、AC于点E、G,连接GF。分析下列结论:①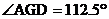 ;②
;②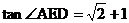 ;③
;③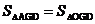 ;④四边形AEFG是菱形;⑤BE=2OG。则其中正确结论的序号是_________。
;④四边形AEFG是菱形;⑤BE=2OG。则其中正确结论的序号是_________。
三、解答题:圆满的解答,是你萌动的智慧,相信你一定表现出色!(本大题共7小题,计64分,解答应写出必要的文字说明,证明过程或演算步骤)
17.(本题满分6分)
计算: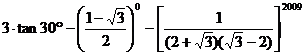
18.(本题满分8分)
2008年北京奥运会刚刚过去,2012年伦敦奥运会已在向世人招手。某校学生会为了了解全校同学最想收看伦敦奥运会哪种比赛项目的情况。随机调查了200名同学,根据调查结果制作了如下频数分布表:
最想收看的项目
频数(人数)
频率
足球
0.14
篮球
36
0.18
排球
16
0.08
羽毛球
30
0.15
乒乓球
游泳
16
0.08
跳水
20
0.10
田径
4
0.02
合计
200
(1)补全频数分布表;
(2)指出这个问题中的个体、总体、样本和样本容量;
(3)在这次抽样调查中,最想收看哪个奥运会比赛项目的同学最多?最想收看哪个比赛项目的同学最少?
(4)根据以上调查,试估计该校5100名学生中,最想收看游泳比赛的人数。
19.(本题满分8分)
某省为解决农村饮用水问题,省财政部门共投资20亿元对各市的农村饮用水的 “改水工程”予以一定比例的补助。2008年,A市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2010年该市计划投资“改水工程”1176万元。
(1)求A市投资“改水工程”的年平均增长率;
(2)从2008年到2010年,A市三年共投资“改水工程”多少万元?
20.(本题满分10分)
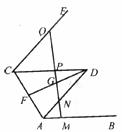
如下图,AB∥CD、AD∥CE,F、G分别是AC和FD的中点,过G的直线依次交AB、AD、CD、CE于点M、N、P、Q,求证:MN+PQ=2PN。
21.(本题满分10分)
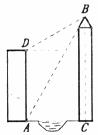
如下图,小丽的家住在某一河畔的电梯公寓AD内,她家的河对岸新建了一座大厦BC。为了测得大厦的高度,小丽在她家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦的顶部B的仰角为30°。已知小丽所住的电梯公寓高82米,请你帮助小丽计算出大厦高度BC及大厦与小丽所住电梯公寓间的距离AC。(计算结果保留根号)
22.(本题满分10分)
如图,已知⊙O1与⊙O2相切于点P,它们的半径分别为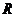 、
、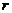 ,一直线绕P点旋转与⊙O1、⊙O2分别交于点A、B(点P、B不重合),探索规律:
,一直线绕P点旋转与⊙O1、⊙O2分别交于点A、B(点P、B不重合),探索规律:
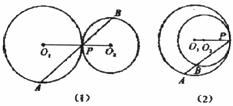
(1)如上图1,当⊙O1与⊙O2外切时。探索 与半径
与半径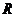 、
、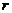 之间的关系式,请证明你的结论;
之间的关系式,请证明你的结论;
(2)如上图2,当⊙O1与⊙O2内切时,第(1)题探求的结论是否成立?为什么?
23.(本题满分12分)
如下图1,在平面直角坐标系中,已知点A(0,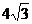 ),点B在
),点B在 正半轴上,且∠ABO=30°。动点P在线段AB上从点A向点B以每秒
正半轴上,且∠ABO=30°。动点P在线段AB上从点A向点B以每秒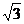 个单位的速度运动,设运动时间为
个单位的速度运动,设运动时间为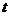 秒。在
秒。在 轴上取两点M,N作等边△PMN。
轴上取两点M,N作等边△PMN。
(1)求直线AB的解析式;
(2)求等边△PMN的边长(用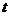 的代数式表示),并求出当等边△PMN的顶点M运动到与原点O重合时
的代数式表示),并求出当等边△PMN的顶点M运动到与原点O重合时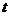 的值;
的值;
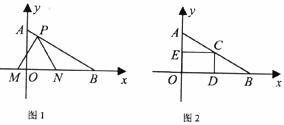
(3)如果取OB的中点D,以OD为边在Rt△AOB内部作如上图2所示的矩形ODCE,点C在线段AB上。设等边△PMN和矩形ODCE重叠部分的面积为S,请求出当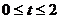 0秒时S与
0秒时S与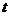 的函数关系式,并求出S的最大值。
的函数关系式,并求出S的最大值。