摘要:(1)求直线AB的解析式,
网址:http://m.1010jiajiao.com/timu_id_757305[举报]
 如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与反比例函数在第三象限内的图象交于点B(-1,n),点C是反比例函数图象上的点,CD⊥x轴于点D,连接CA、CO,tan∠COD=cos∠ACD,AC=2.5,AD:CD=3:4.
如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与反比例函数在第三象限内的图象交于点B(-1,n),点C是反比例函数图象上的点,CD⊥x轴于点D,连接CA、CO,tan∠COD=cos∠ACD,AC=2.5,AD:CD=3:4.(1)求该反比例函数的解析式;
(2)求直线AB的解析式.
如图,已知点A(3,m),B(n,6)在反比例函数y=-
的图象上,直线AB与x轴交于点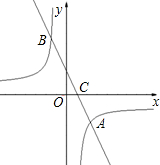 C,如果点D在坐标轴上,且OA=DC.
C,如果点D在坐标轴上,且OA=DC.
(1)写出A,B两点的坐标;
(2)求直线AB的解析式;
(3)求点D的坐标. 查看习题详情和答案>>
| 12 | x |
 C,如果点D在坐标轴上,且OA=DC.
C,如果点D在坐标轴上,且OA=DC.(1)写出A,B两点的坐标;
(2)求直线AB的解析式;
(3)求点D的坐标. 查看习题详情和答案>>
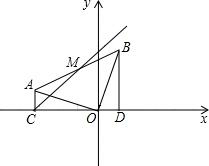
在平面直角坐标系中,△AOC中,∠ACO=90°.把AO绕O点顺时针旋转90°得OB,连接AB,作BD⊥直线CO于D,点A的坐标为(-3,1).
(1)求直线AB的解析式;
(2)若AB中点为M,连接CM,动点P、Q分别从C点出发,点P沿射线CM以每秒
个单位长度的速度运动,点Q沿线段CD以每秒1个长度的速度向终点D运动,当Q点运动到D点时,P、Q同时停止,设△PQO的面积为S(S≠0),运动时间为T秒,求S与T的函数关系式,并直接写出自变量T的取值范围;
(3)在(2)的条件下,动点P在运动过程中,是否存在P点,使四边形以P、O、B、N(N为平面上一点)为顶点的矩形?若存在,求出T的值.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求直线AB的解析式;
(2)若AB中点为M,连接CM,动点P、Q分别从C点出发,点P沿射线CM以每秒
| 2 |
(3)在(2)的条件下,动点P在运动过程中,是否存在P点,使四边形以P、O、B、N(N为平面上一点)为顶点的矩形?若存在,求出T的值.
 查看习题详情和答案>>
查看习题详情和答案>>
 (2012•聊城)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(2012•聊城)如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).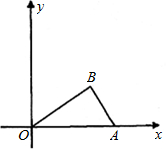 为
为