2008-2009学年度泰安市肥城第二学期初三期中考试
数学试卷
时间:120分钟 满分:120分
1.本试题分第Ⅰ卷和第Ⅱ卷两部分。第Ⅰ卷2页为选择题,36分;第Ⅱ卷4页为非选择题,84分;全卷共6页,满分120分,考试时间为120分钟。
2.考试时,不允许使用科学计算器。
一、选择题(本大题共12题,每小题3分,共36分)下列各题的四个结论中只有一个是正确的,请将正确答案填入下表。
1.sin30°的值是 ( )
A.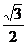 B.
B.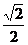 C.
C.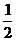 D.1
D.1
2.抛物线y=(x?2)2的顶点坐标是 ( )
A.(2,0) B.(-2,0) C.(0,2) D.(0,-2)
3.如果⊙O1和⊙O2的半径分别为
( )
A.外离 B.外切 C.相交 D.内切
4.二次函数y=x2的图像向上平移2个单位,得到新的图像的二次函数表达式是 ( )
A.y=x2?2 B.y=(x?2)
5.图中∠BOD的度数是 ( )
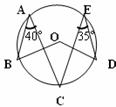
A.75° B.80° C.135° D.150°
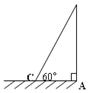
6.等腰三角形的腰长与底边之比为1:,则底角和顶角的度数分别是 ( )
A.30°和120° B.45°和90° C.60°和60° D.15°和150°
7.如图,一电线杆AB的高为
(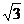 取1.732,结果保留3个有效数字)
取1.732,结果保留3个有效数字)
A.
8.已知抛物线y =ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①a、b同号;② 当x=1和x=3时,函数值相等;③
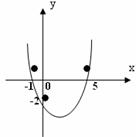
A.1个 B.2个 C.3个 D.4个
9.如图,已知AD是△ABC的外接圆的直径,AD=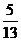 ,则AC的长等于( )
,则AC的长等于( )

A.
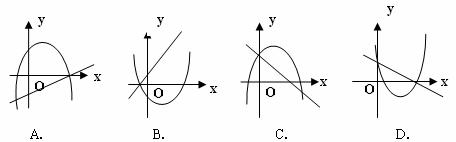
10.已知一次函数y =ax+c与二次函数y =ax2+bx+c,它们在同一坐标系内的大致图像是
( )
11.如图,实线部分是半径为
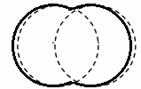
A.12πm B.18πm C.20πm D.24πm
12.如图,⊙O是正方形ABCD的外接圆,F是AD的中点,CF的延长线交⊙O于E,那么CF∶EF的值是 ( )

A.3∶1 B.4∶
 二.填空题(本大题共8小题,每小题3分,共24分)
二.填空题(本大题共8小题,每小题3分,共24分)
13.计算: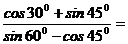
14.抛物线y = x 2-4 x +5的对称轴是 .
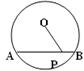
15.如图,已知⊙O的半径为5,弦AB=8,P是弦AB上一动点,则OP的取值范围是 .
16.在Rt△ABC中,∠C=90°,AB=5,AC=3,则sinB= .
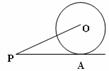
17.如图,⊙O的半径为1,PA切⊙O于点A,且PA=2,则tan∠APO的值为 .
18.一元钱硬币的直径约为
mm.(保留根号)
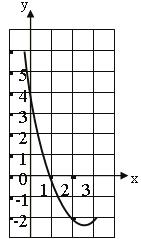
19.如图是某抛物线y =ax2+bx+c的部分图象,有图象可知一元二次方程ax2+bx+c=0的两个解分别是 和 .
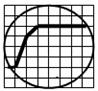
20.如图所示,圆被一条折线(图中粗线)所分成的两部分面积之差为 .
(网格由边长为1的正方形构成)
三、解答题(本题共6小题,共60分)
21.(本小题8分)A、B两个口袋中都有三个相同的小球,分别标有1、2、3,小刚、小丽两人进行摸球游戏,游戏规则是:小刚从A袋中随机摸一个球,同时小丽从B袋中随机摸一个球,当两个球上所标数字之和为奇数是小刚赢,否则小丽赢,这个游戏对双方公平吗?通过列表或画树状图加以说明.
22.(本小题8分)如图所示,在广场上A点放一个气球,当气球上升
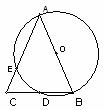
23.(本小题8分)如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,连结AC交⊙O于E,
(1)则BD与CD的大小有什么关系?说明理由;
(2)若∠C=680,连结OE,则圆心角∠AOE的度数是多少?为什么?
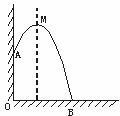
24.(12分)某幢建筑物,从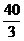 m,
m,
(1)在图形中建立适当的直角坐标系,求出水流呈抛物线的解析式;
(2)则水流落地点B离墙的距离OB是多少?
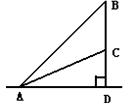
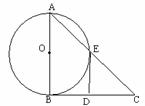
25.(12分)如图所示,△ABC是直角三角形,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边的中点,连接DE
(1)求证:DE与⊙O相切
(2)若⊙O的半径为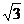 ,DE=3,求AE.
,DE=3,求AE.
26.(12分)
某科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代品,并投入资金1500万元进行批量生产,已知生产每件产品的成本为40元,在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价没增加10元。年销售量将减少1万件,设销售单价为x元,年销售量为y万件,年获利为z万元;
(1)求y与x之间的函数关系式;
(2)求z与x之间的函数关系式;
(3)当销售单价定为多少时,年获利最大,为多少?