2008-2009学年度菏泽郓城县第一学期九年级初中教学质量检测
数学试卷
说明:本试题满分为120分,考试时间为120分钟。
一、选择题(每小题给出的四个选项中,只有一个是正确的。每小题得2分,共18分)
1.如果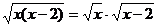 ,那么
,那么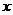 的取值范围是( )
的取值范围是( )
A.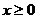 B.
B.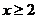
C.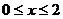 D.
D.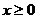 或算
或算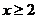
2.关于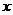 的一元二次方程
的一元二次方程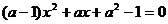 的一个根为0,则
的一个根为0,则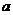 的值为( )
的值为( )
A.-1 B.0 C.1 D.±1
3.如下图,D是等腰Rt△ABC内一点,AB是斜边,如果将△BCD绕点C逆时针方向旋转到 的位置,则
的位置,则 的度数是( )
的度数是( )
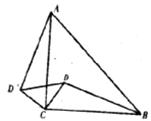
A.30° B.35° C.40° D.45°
4.如下图,⊙O的弦AB、CD交于P,∠B=30°,∠APD=70°,则∠CAB的度数为( )
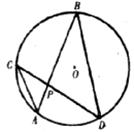
A.30° B.40° C.50° D.60°
5.如下图,在□ABCD的一边AB为直径作⊙O,且使点C在⊙O上,若∠AOC=70°,则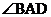 的度数为( )
的度数为( )
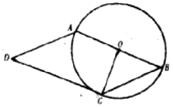
A 120° B.130° C.140° D.145°
6.如果一个正多边形的每个外角都等于36°,那么这个正多边形的中心角的度数是( )
A.36° B.60° C.72° D.80°
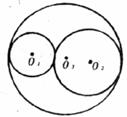
7.如下图,⊙O1与⊙O2相外切,⊙O1与⊙O2又都与⊙O3相内切,设⊙O1的周长为P1,⊙O2的周长为P2,⊙O3的周长为P3,那么有( )
A.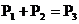 B.
B.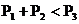
C.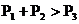 D.
D.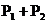 与
与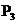 的大小关系不能确定
的大小关系不能确定
8.下列函数中是二次函数的是( )
A.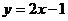 B.
B.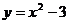 C.
C.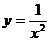 D.
D.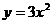
9.二次函数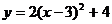 的图像的开口方向、对称轴和顶点坐标分别为( )
的图像的开口方向、对称轴和顶点坐标分别为( )
A.开口向上,对称轴是直线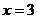 ,顶点坐标是(3,4)
,顶点坐标是(3,4)
B.开口向上,对称轴是直线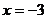 ,顶点坐标是(-3,4)
,顶点坐标是(-3,4)
C.开口向下,对称轴是直线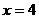 ,顶点坐标是(3,-4)
,顶点坐标是(3,-4)
D.开口向下,对称轴是直线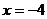 ,顶点坐标是(-4,-3)
,顶点坐标是(-4,-3)
二、填空题(每空3分,共30分)
1.写出两个二次根式,使这两个二次根式的积为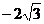 ,这两个二次根式为___________。
,这两个二次根式为___________。
2.一个三角形的一条边长为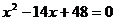 的两个实数根,则这个三角形最大内角的度数___________。
的两个实数根,则这个三角形最大内角的度数___________。
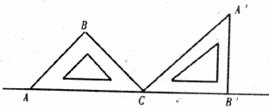
3.如下图所示,一块等腰直角三角板ABC在水平桌面上绕点C按顺时针方向旋转到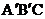 的位置,点A、C、
的位置,点A、C、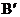 均在水平桌面上,那么旋转的角度为___________。
均在水平桌面上,那么旋转的角度为___________。
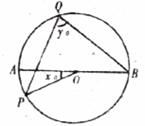
4.如下图,AB为⊙O的直径,点P为半圆上不与A、B重合的一点,点Q为另一半圆上的一个定点,如果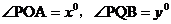 ,则
,则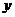 与
与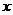 之间的函数关系式为___________。
之间的函数关系式为___________。
5.同一个圆的内接正方形和外切正六边形的边长之比为___________。
6.如下图,两个相等的圆环的圆心分别为O1、O2,它们的外圆交于A、B两点,且四边形O1AO2B恰为正方形,已知内圆的半径为
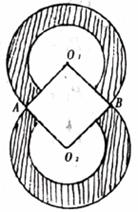
7.现有长度分别为
8.抛物线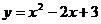 与
与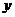 轴交点的坐标是___________。
轴交点的坐标是___________。
9.二次函数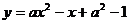 的图像如下图所示,则
的图像如下图所示,则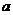 的值为___________。
的值为___________。
10.写出一个开口向上,对称轴为直线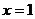 ,且与
,且与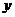 轴的交点坐标为(0,2)的抛物线的解析式:___________。
轴的交点坐标为(0,2)的抛物线的解析式:___________。
三、每小题4分,共8分。
1.化简: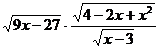
2.先化简,再求值: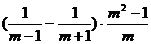 ,其中
,其中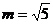
四、本题8分。
当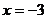 时,二次三项式
时,二次三项式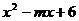 的值为0,当
的值为0,当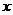 为何值时,这个二次三项式的值为12。
为何值时,这个二次三项式的值为12。
五、本题8分。
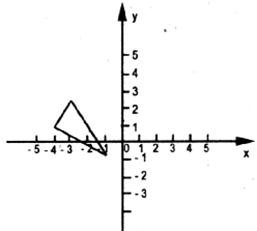
如下图,△ABC在平面直角坐标系内,点A、B、C的坐标分别为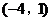 、
、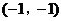 、
、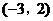 ,作出与△ABC关于原点对称的图形,并指出点A、B、C的对称点
,作出与△ABC关于原点对称的图形,并指出点A、B、C的对称点 的坐标。
的坐标。
六、本题8分。
已知,⊙O的直径AB=
七、本题8分。
掷两枚硬币,求下列事件的概率:
(1)两枚硬币全部正面朝上;
(2)一枚硬币正面朝上,另一枚硬币反面朝上。
八、本题8分。
画出函数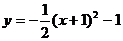 的图像,指出它的最高点的坐标,并说出这条抛物线经过怎样平移可以得到抛物线
的图像,指出它的最高点的坐标,并说出这条抛物线经过怎样平移可以得到抛物线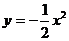 。
。
九、本题10分。
如下图,在△ABC中,∠ABC=90°,AB=
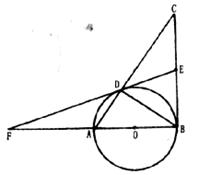
(1)直线DE与⊙O的位置关系如何?证明你的结论;
(2)求BD的长。
十、本题12分。
如下图,以A(0,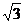 )为圆心的圆与
)为圆心的圆与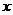 轴相切于坐标原点O,与
轴相切于坐标原点O,与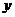 轴交于点B,弦BD的延长线交
轴交于点B,弦BD的延长线交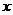 轴的负半轴于点E,∠BEO=60°,AD的延长线交
轴的负半轴于点E,∠BEO=60°,AD的延长线交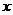 轴于点C。
轴于点C。
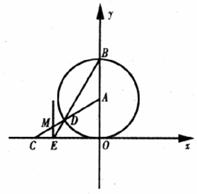
(1)求点E和点C的坐标;
(2)求经过A、C两点,且以过E点而平行于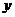 轴的直线为对称轴的抛物线的解析式;
轴的直线为对称轴的抛物线的解析式;
(3)设抛物线的对称轴与AC的交点为M,试判断以点M为圆心、ME为半径的圆与⊙A的位置关系,并说明理由。