摘要:画出函数的图像.指出它的最高点的坐标.并说出这条抛物线经过怎样平移可以得到抛物线.九.本题10分.如下图.在△ABC中.∠ABC=90°.AB=6cm.BC=8cm.以AB为直径的⊙O交AC于D.E是BC的中点.连结ED并延长交BA的延长线于F.
网址:http://m.1010jiajiao.com/timu_id_748757[举报]
26、有一个水箱,它的容积500升,水箱内原有水200升,现需将水箱注满,已知每分钟注入水10升.
(1)写出水箱内水量Q(升)与时间t(分)的函数关系式;
(2)求自变量t的取值范围;
(3)画出函数的图象.
查看习题详情和答案>>
(1)写出水箱内水量Q(升)与时间t(分)的函数关系式;
(2)求自变量t的取值范围;
(3)画出函数的图象.
请你在所学课本里的函数中选择一个函数,使它的图象经过点A(1,3)和B(3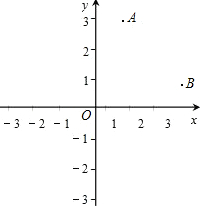 ,1).
,1).
(1)求出所选函数的解析式,并画出函数的图象;
(2)根据图象,说出函数的三条性质(或图象的特征). 查看习题详情和答案>>
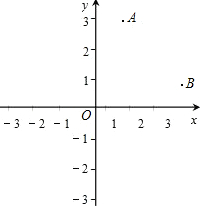 ,1).
,1).(1)求出所选函数的解析式,并画出函数的图象;
(2)根据图象,说出函数的三条性质(或图象的特征). 查看习题详情和答案>>
 问题情境
问题情境已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+
| a |
| x |
探索研究
(1)我们可以借鉴学习函数的经验,先探索函数y=x+
| 1 |
| x |
1填写下表,画出函数的图象:
| x | … |
|
|
|
1 | 2 | 3 | 4 | … | ||||||
| y | … | … |
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,除了通过观察图象,还可以通过配方得到.同样通过配方也可以求函数y=x+
| 1 |
| x |
| 1 |
| x |
| x |
|
| x |
|
| x |
|
| x |
|
=(
| x |
|
当
| x |
|
| 1 |
| x |
解决问题
(2)解决“问题情境”中的问题,直接写出答案.
【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+
)(x>0).
【探索研究】
(1)我们可以借鉴以前研究函数的经验,先探索函数y=x+
(x>0)的图象和性质.
①填写下表,画出函数的图象;
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数y=x+
(x>0)的最小值.
【解决问题】
(2)用上述方法解决“问题情境”中的问题,直接写出答案. 查看习题详情和答案>>
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+
| a |
| x |
【探索研究】
(1)我们可以借鉴以前研究函数的经验,先探索函数y=x+
| 1 |
| x |

①填写下表,画出函数的图象;
| x | … |
|
|
|
1 | 2 | 3 | 4 | … | ||||||
| y | … | … |
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数y=x+
| 1 |
| x |
【解决问题】
(2)用上述方法解决“问题情境”中的问题,直接写出答案. 查看习题详情和答案>>