2008-2009学年度潍坊市昌邑初中学段第一学期九年级期末考试
数学试卷
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请将正确答案的序号填写在题后的括号内,每小题3分,共33分)
1.方程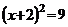 的解是( )
的解是( )
A.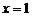 B.
B.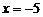 C.
C.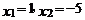 D.
D.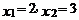
2.在Rt△ABC中,∠C=90°,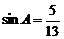 ,则
,则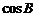 =( )
=( )
A.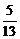 B.
B.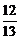 C.
C.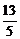 D.
D.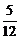
3.如图,梯形护坝的斜坡AB坡度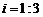 ,坝高BC为
,坝高BC为
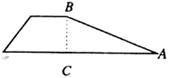
A.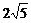 米 B.
米 B.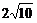 米 C.
米 C.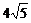 米 D.
米 D.
4.如图,为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进
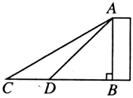
A.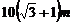 B.
B.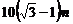 C.
C.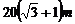 D.
D.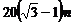
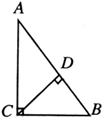
5.如图,CD是Rt△ABC斜边上的高,AC=4,BC=3,则cos∠BCD的值为( )
A.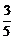 B.
B.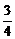 C.
C.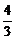 D.
D.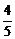
6.二次函数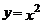 的图象向左平移4个单位,再向上平移3个单位,得到的新的图象的函数表达式是( )
的图象向左平移4个单位,再向上平移3个单位,得到的新的图象的函数表达式是( )
A.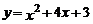 B.
B.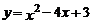
C. D.
D.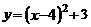
7.把二次函数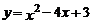 化成
化成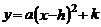 的形式是( )
的形式是( )
A.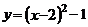 B.
B.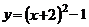
C.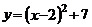 D.
D.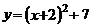
8.在反比例函数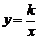 中,当
中,当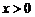 时,
时,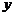 随
随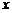 地增大而减小,则二次函数
地增大而减小,则二次函数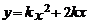 图象大致是下图中的( )
图象大致是下图中的( )
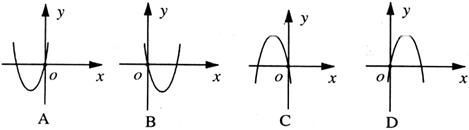
9.函数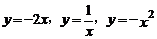 的共同性质是( )
的共同性质是( )
A.它们的图象都经过原点
B.它们的图象都不经过第二象限
C.在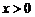 的条件下,
的条件下,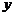 都随
都随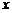 的增大而增大
的增大而增大
D.在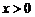 的条件下,
的条件下,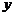 都随
都随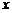 的增大而减小
的增大而减小
10.袋中有同样大小的4个小球,其中3个红色,1个白色,从袋中任意地同时摸出两个球,这两个球颜色相同的概率是( )
A.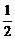 B.
B.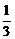 C.
C.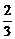 D.
D.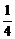
11.下列说法中正确的有( )
(1)在标有1至100号的100张卡片中随机抽取一张,抽到2号卡片的概率是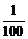 ;
;
(2)袋子里装有红、白、黑三种颜色的球,随手拿出一个球,恰好是红球的概率是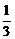 ;
;
(3)同时抛掷两枚硬币,反面都向上的概率为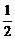 ( )
( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每小题3分,共27分)
12.要使二次根式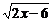 有意义,
有意义,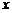 应满足的条件是__________.
应满足的条件是__________.
13.若关于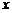 的一元二次方程
的一元二次方程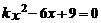 有两个不相等的实数根,则
有两个不相等的实数根,则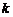 的取值范围____.
的取值范围____.
14.在Rt△ABC中,若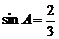 ,则
,则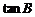 =__________.
=__________.
15.△ABC的三条边长分别是2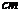 、5
、5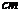 和6
和6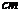 ,与其相似的另一个
,与其相似的另一个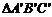 的最大边长为18
的最大边长为18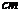 ,那么它的最小边长为_________,较小三角形与较大三角形周长的比是_________.
,那么它的最小边长为_________,较小三角形与较大三角形周长的比是_________.
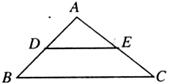
16.如图,DE是△ABC的中位线,△ADE的面积为5 2,则四边形DBCE的面积为_______.
2,则四边形DBCE的面积为_______.
17.我市的住宅电话号码由7位数字组成,某人要安装一部住宅电话,电话的号码末尾数字为8的概率是__________.
18.抛物线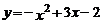 与
与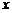 轴的交点坐标是_________,与
轴的交点坐标是_________,与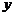 轴的交点坐标是________.
轴的交点坐标是________.
19.二次函数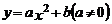 中,若当
中,若当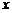 取
取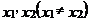 时函数值相等,则当
时函数值相等,则当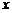 取
取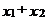 时,函数值等于__________.
时,函数值等于__________.
20.某市今年1月份的工业产值达5亿元,第一季度的总产值是16.55亿元,若设后两个月的产值平均月增长的百分率是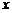 ,则根据题意可以列出方程是____________________.
,则根据题意可以列出方程是____________________.
三、解答题(解答应写出必要的计算过程、推演步骤或文字说明)
21.(8分)求下列式子的值
(1)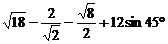
(2)
22.(5分)已知二次函数的图象的对称轴为直线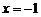 ,函数的最大值为4,且图象经过点(2,-5),求此函数的关系式.
,函数的最大值为4,且图象经过点(2,-5),求此函数的关系式.
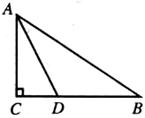
23.(6分)如图所示,在Rt△ABC中,∠C=90°,AD为角平分线,AC=15,AD=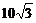 ,求直角边BC和斜边AB的长.
,求直角边BC和斜边AB的长.
24.(8分)抛物线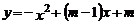 与
与 轴交于(0,3)点.
轴交于(0,3)点.
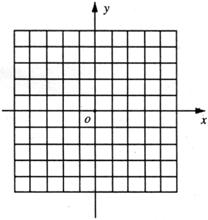
(1)求出 的值并画出这条抛物线;
的值并画出这条抛物线;
(2) 取什么值时,抛物线在
取什么值时,抛物线在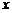 轴上方?
轴上方?
(3)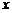 取什么值时,
取什么值时,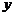 随
随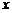 的增大而减小?
的增大而减小?
25.(8分)如图所示,小明的眼睛D距离地面高度AD=
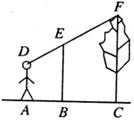
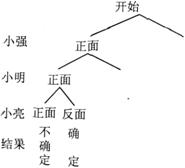
26.(7分)小强、小明和小亮三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,游戏规则如下:三人手中各持有一枚质地均匀的硬币,‘他们同时将手中硬币抛落到水平地面为一个回合。落地后,三枚硬币中,恰有两枚正面向上或者反面向上的两人先下棋;若三枚硬币均为正面向上或反面向上,则不能确定其中哪两人先下棋.
(1)请你完成下面表示游戏一个回合所有可能出现的结果的树状图;
(2)求一个回合能确定两人先下棋的概率。
解:(1)树状图为:
27.(8分)如图,在观测点E测得小山上铁塔顶A点仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20 ,观测点E到地面的距离EF=35
,观测点E到地面的距离EF=35 ,求小山BD的高。(结果保留根号)
,求小山BD的高。(结果保留根号)

28.(10分)某汽车销售商销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价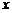 万元,每辆汽车的销售利润为
万元,每辆汽车的销售利润为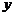 万元。(销售利润=销售价-进货价)
万元。(销售利润=销售价-进货价)
(1)求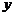 与
与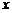 的函数关系式;在保证商家不亏本的前提下,写出
的函数关系式;在保证商家不亏本的前提下,写出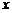 的取值范围;
的取值范围;
(2)假设这种汽车平均每周的销售利润为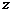 万元,试写出
万元,试写出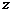 与
与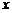 之间的函数关系式;
之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?