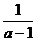2008年安徽淮北西园中学中考第二次模拟考试
数学试卷
一、选择题(本题共10小题,每小题4分,满分40分)
A.±4 B
2,
3,把不等式组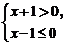 的解集表示在数轴上,如图1,正确的是( )
的解集表示在数轴上,如图1,正确的是( )

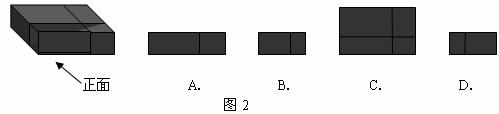
4,2008中国(淮北)专利技术推介会在我市隆重开幕,下(左)图2是会展中心搭成的展台,图中所示展台的主视图是( )
5,如图3,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于( )
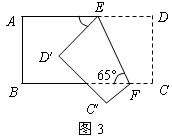
A.50° B.55° C.60° D.65°
6,如图4,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
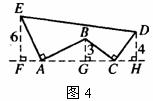
A.50 B
7,已知:如图5,点G是BC的中点,点H在AF上,动点P以每秒
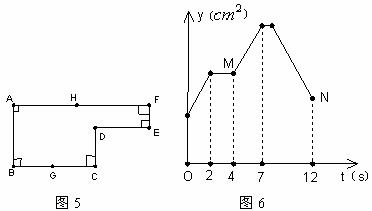
A.1个 B.2个 C.3个 D.4个
8,如图7,P1、P2、P3是双曲线上的三点.过这三点分别作y轴的垂线,得到三个三角形△P
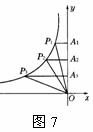
A.S1<S2<S3 B.S2<S1<S
9,如图8,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连结AC、BD,则图中阴影部分的面积为( )
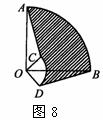
A. 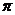 B.
B. 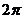 C.
C. 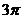 D.
D. 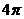
二、填空题(本题共4小题,每小题5分,满分20分)
11,某住宅小区6月份随机抽查了该小区6天的用水量(单位:吨),结果分别是30、34、32、37、28、31,那么,请你估计该小区6月份(30天)的总用水量约是 吨.
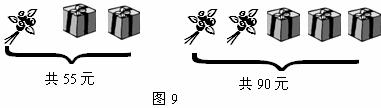
12、母亲节那天,很多同学给妈妈准备了鲜花和礼盒.从如图9中信息可知一束鲜花的价格是___元.
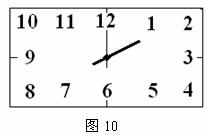
13,如图10为长方形时钟钟面示意图,时钟的中心在长方形对角线的交点上,长方形的宽为20厘米,钟面数字2在长方形的顶点处,则长方形的长为___厘米.
14,在数学中,为了简便,记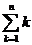 =1+2+3+…+(n-1)+ n.1!=1,2!=2×1,3!=3×2×1,…,n!=n×(n-1)×(n-2)×…×3×2×1.则
=1+2+3+…+(n-1)+ n.1!=1,2!=2×1,3!=3×2×1,…,n!=n×(n-1)×(n-2)×…×3×2×1.则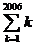 -
-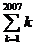 +
+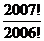 =___.
=___.
三、(本题共2小题,每小题8分,满分16分)
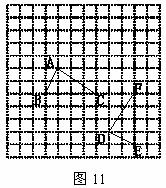
(1)图中的格点△DEF是由格点△ABC通过怎样的变换得到的?(写出变换过程)
(2)根据你写出的变换过程,求出点A经过的路线长。
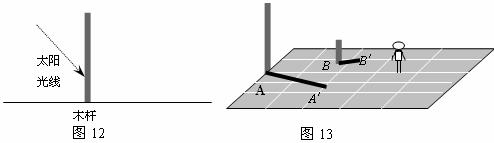
17,(1)一木杆按如图12所示的方式直立在地面上,请在图中画出它在阳光下的影子(用线段CD表示);
(2)如图13是两根标杆及它们在灯光下的影子.请在图中画出光源的位置(用点P表示);并在图中画出人在此光源下的影子(用线段EF表示).
四、(本题共2小题,每小题8分,满分16分)
18,图14是某区近期卖出的不同户型的商品房中随机抽取1000套进行统计,并根据统计结果绘出如图所示的统计图,请结合统计图提供的信息,解答下列问题:
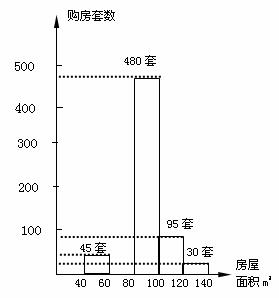
(1)卖出面积为60~80平方米的商品房多少套?并补全统计图;
(2)请写出该组数据的中位数所在的范围;
(3)求面积在什么范围内的住房卖出最多?约占全部卖出住房的百分之几?
五.(本题共2小题,每小题10分,满分20分)
19, 如图15,某学校九年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“

(1)小军能进入迷宫中心的概率是多少?请画出树状图进行说明.
(2)小组两位组员小张和小李商量做一个小游戏,以猜测小军进迷宫的结果比胜负.游戏规则规完:小军如果能进入迷宫中心,小张和小李各得1分;小军如果不能进入迷宫中心,则他在最后一个进口处所得乘积是奇数时,小张得3分,所得乘积是偶数时,小李得3分,你认为这个游戏公平吗?如果公平,请说明理由;如果不公平,请在第二道环进口处的两个数中改变其中一个数使游戏公平.
(3)在(2)的游戏规则下,让小军从最外环进口任意进入10次,最终小张和小李的总得分之和不超过28分,请问小军至少几次进入迷宫中心?
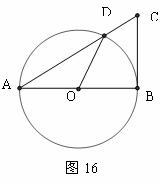
20, 如图16,在ㄓABC中,以AB为直径的⊙O与AC相交于点D,已知AB=10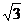 ,CD=5,∠BOD=600
,CD=5,∠BOD=600
(1)求证:BC是⊙O的切线。
(2)求ㄓABC与⊙O重合部分的面积。
六.(本题满分12分)
21,如图17是按一定规律排列的方程组集合和它解的集合的对应关系图,若方程组处左至右依次记作方程组1、方程组2、方程组3、……方程组n.
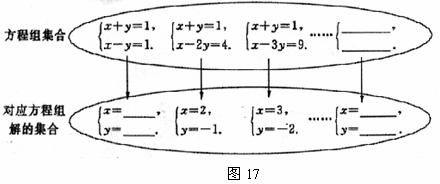
(1)将方程组1的解填入图中;
(2)请依据方程组和它的解变化的规律,将方程组n和它的解直接填入集合图中;
(3)若方程组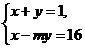 的解是
的解是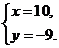 求m的值,并判断该方程组是否符合(2)中的规律?
求m的值,并判断该方程组是否符合(2)中的规律?
七.(本题满分12分)
22,操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图18,19,20是旋转三角板得到的图形中的3种情况.
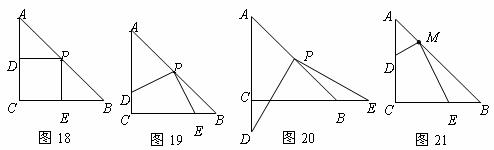
探究:(1)三角板绕点P旋转,通过观察或测量,猜想线段PD和PE之间有什么数量关系?并结合图19加以证明.
(2)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,写出△PBE的腰长;若不能,请说明理由.
(3)若将三角板的直角顶点放在斜边AB上的M处,且AM∶MB=1∶3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合图21加以证明.
八.(本题满分14分)
23,已知抛物线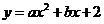 与
与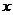 轴相交于点
轴相交于点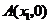 ,
,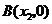
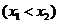 ,且
,且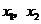 是方程
是方程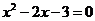 的两个实数根,点
的两个实数根,点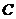 为抛物线与
为抛物线与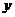 轴的交点.
轴的交点.
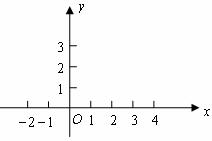
(1)求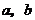 的值;
的值;
(2)分别求出直线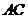 和
和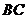 的解析式;
的解析式;
(3)若动直线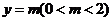 与线段
与线段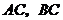 分别相交于
分别相交于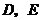 两点,则在
两点,则在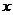 轴上是否存在点
轴上是否存在点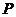 ,使得
,使得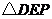 是等腰直角三角形?若存在,求出点
是等腰直角三角形?若存在,求出点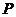 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.