2008-2009学年度潍坊市奎文区第一学期八年级期中考试
数学试卷
时间:90分钟 总分:120分
一、选择题(共10个小题,每小题3分,共30分)
1.4的平方根是( ).
A.8 B.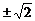
2.已知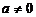 ,
,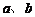 互为相反数,则下面各组数中,不是互为相反数的一组是( ).
互为相反数,则下面各组数中,不是互为相反数的一组是( ).
A.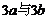 B.
B.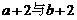 C.
C.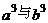 D.
D.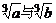
3.估算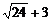 的值( )
的值( )
A.在5和6之间 B.在6和7之间 C.在7和8之间 D.在8和9之间
4.下列运算正确的是( )
A. B.
B. C.
C.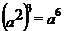 D.
D.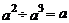
5.关于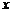 的一次二项式
的一次二项式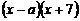 的积中的常数项为14,则
的积中的常数项为14,则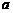 的值是( ).
的值是( ).
A.2 B.-2 C.7 D.-7
6.如下图,有一张直角三角形纸片,两直角边AC=4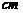 ,BC=8
,BC=8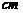 ,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为( ).
,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为( ).
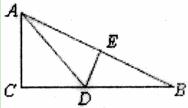
A.5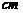 B.4
B.4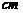 C.3
C.3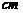 D.3.75
D.3.75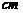
7.若一个直角三角形的三边长分别为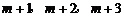 ,则
,则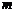 的值为( ).
的值为( ).
A.2 B.4 C.9 D.16
8.实数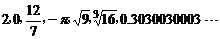 中,无理数的个数有( ).
中,无理数的个数有( ).
A.2个 B.3个 C.4个 D.5个
9.若直角三角形的三边长分别为2、4、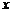 ,则
,则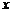 的所有可能值是( ).
的所有可能值是( ).
A.20、12 B.5、3 C.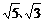 D.
D.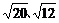
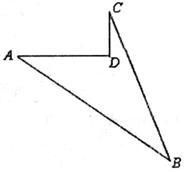
10.如下图,已知AB:BC:CD:DA=2:2:3:1,且∠ABC=90°,那么∠DAB的度数为( ).
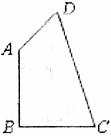
A.120° B.130° C.135。° D.145°
二、填空题(共10个小题,每小题3分,共30分)
11.8的立方根是__________.
12.计算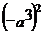 =__________.
=__________.
13.若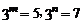 ,则
,则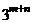 =__________.
=__________.
14.1千克镭完全蜕变后,放出的热量相当于3.75×105千克煤放出的热量,据估计地壳里含1×1010千克镭.这些镭完全蜕变后放出的热量相当于__________千克煤放出的热量.
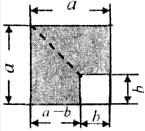
15.如下图是由边长为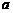 和
和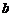 的两个正方形组成,通过用不同的方法,计算图中阴影部分的面积,可以验证的一个公式是____________________.
的两个正方形组成,通过用不同的方法,计算图中阴影部分的面积,可以验证的一个公式是____________________.
16.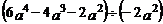 =__________.
=__________.
17.若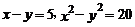 ,则
,则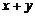 =__________.
=__________.
18.如果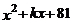 是一个完全平方式,那么
是一个完全平方式,那么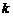 的值是__________.
的值是__________.
19.已知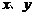 为正数,且
为正数,且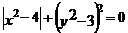 ,如果以
,如果以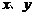 的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积是__________.
的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积是__________.
20.大家一定熟知杨辉三角(Ⅰ),观察下列等式(Ⅱ)
1
1 1 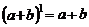
1 2 1 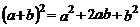
1 3 3 1 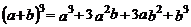
1 4 6 4 1 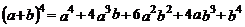
……………………………………………………
Ⅰ Ⅱ
根据前面各式规律,则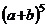 =__________.
=__________.
三、解答题(共7个小题,共60分)
21.(1)计算:(每小题3分,共6分)
①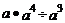
②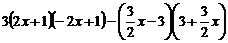
(2)分解因式:(每小题3分,共6分)
①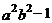
②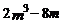
22.先化简,再求值: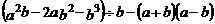 ,其中
,其中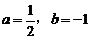 .
.
23.(8分)如下图所示的一块地,已知AD=4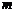 ,CD=3
,CD=3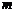 ,AD⊥DC,AB=13
,AD⊥DC,AB=13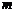 ,BC=12
,BC=12 ,求这块地的面积.
,求这块地的面积.
24.(8分)如下图所示,在长和宽分别是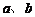 的矩形纸片的四个角都剪去一个边长为
的矩形纸片的四个角都剪去一个边长为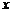 的正方形.
的正方形.
(1)用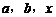 表示纸片剩余部分的面积.
表示纸片剩余部分的面积.
(2)当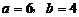 ,且剪去部分的面积等于剩余部分的面积时,求正方形的边长
,且剪去部分的面积等于剩余部分的面积时,求正方形的边长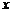 .
.

25.(8分)已知: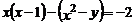 ,求
,求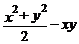 的值.
的值.
26.(8分)2002年8月在北京召开的国际数学家大会会标如下图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是7,小正方形的面积是1,直角三角形的较长直角边为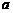 ,较短直角边为
,较短直角边为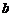 .
.
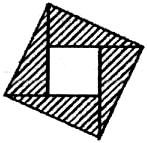
求:(1)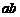 的值:(2)
的值:(2)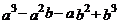 的值.
的值.
27.(10分)如下图所示的长方体是某种饮料的纸质包装盒,规格为5×6×10(单位: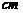 ),在上盖中开有一孔便于插吸管,吸管长为13
),在上盖中开有一孔便于插吸管,吸管长为13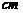 ,小孔到图中边AB距离为1
,小孔到图中边AB距离为1 ,到上盖中与AB相邻的两边距离相等,已知插入吸管后露在盒外面的管长为
,到上盖中与AB相邻的两边距离相等,已知插入吸管后露在盒外面的管长为
 .
.
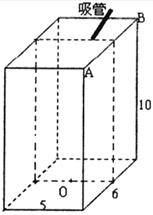
(1)若吸管最下端恰好在包装盒底部的正中央点O时,求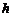 的值;
的值;
(2)试求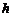 的最小值大约是多少?
的最小值大约是多少?
(参考数据: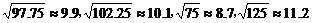 )
)