2007-2008学年度烟台市招远第二学期初一期末考试
数学试卷
说明:
1.本试卷试题共115分;
2.书写质量3分;
3.卷面安排2分;
整个试卷满分为120分。
一、选择题:(将唯一正确答案代号填在括号内。每小题2分,满分30分)
1.对于用四舍五入得到近似数0.4708,下列说法正确的是
A.精确到万分位,有3个有效数字 B.精确到万分位,有4个有效数字
C.精确到十万分位,有3个有效数字 D.精确到十万分位,有4个有效数字
2.三角形的三条高所在的直线相交于一点,则这个交点的位置
A.在三角形外 B.在三角形内
C.在三角形边上 D.要根据三角形的形状才能定
3.下列运算正确的是
A.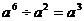 B.
B.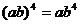
C.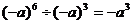 D.
D.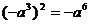
4.如下图,平行的两幢大楼顶部各有一个射灯,当光柱相交时,∠1+∠2+∠3等于

A.180° B.270° C.360° D.450°
5.现有长为
A.1个 B.2个 C.3个 D.4个
6.掷一个均匀的小正方体,这个小正方体的每个面上分别标有数字1,2,3,4,5,6。任意掷出小正方体后,可能性最大的是
A.朝上的数字是5 B.朝上的数字是偶数
C.朝上的数字是奇数 D.朝上的数字小于5
7.如下图,AB∥CD,EG⊥AB,垂足为G,若∠1=58°,则∠E度数等于
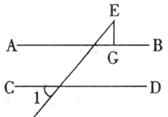
A.58° B.32° C.29° D.22°
8.小明给在北京的姑姑打电话,电话费随时间的变化而变化,在这个问题中,因变量是
A.时间 B.电话费 C.电话 D.距离
9.张华用最小刻度单位是毫米的直尺测量一本书的长度,他量得的数据是
A.9和5是精确的,8是估计的 B.9是精确的,5和8是估计的
C.9、5和8都是精确的 D.9、5和8都是估计的
10.一个两边平行的纸条,如下图那样折叠一下,则∠1的度数是
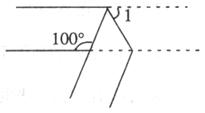
A.30° B.40° C.50° D.60°
11.如图,AB=AD,∠BAO=∠DAO,由此可以得出的全等三角形是
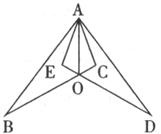
A.△ABC≌△ADE B.△ABO≌△ADO
C.△AEO≌△ACO D.△ABC≌△ADO
12.若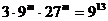 ,则
,则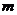 的值为
的值为
A.3 B.
13.如果一盒圆珠笔有12支,售价18元,用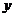 (元)表示圆珠笔的售价,
(元)表示圆珠笔的售价,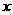 表示圆珠笔的支数,那么
表示圆珠笔的支数,那么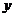 与
与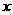 之间的关系应为
之间的关系应为
A.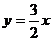 B.
B.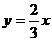 C.
C.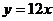 D.
D.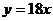
14.如下图,点B、F在CD上,∠C=∠D=90°,AB=EF,CF=BD,若∠A=35°,则∠DFE等于
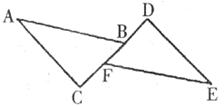
A.35° B.45° C.55° D.65°
15.学校水塔蓄水
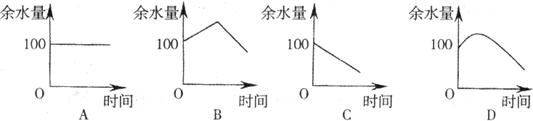
二、填空题:(将正确答案填在横线上,每小题3分,满分30分)
16.一种病毒长度约为
17.如下图,在△ABD中,∠D=90°,AC是角平分线,CD=
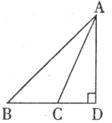
18.小明任意买一张电影票,座位号是偶数与座位号是3的倍数中, 的可能性较大。
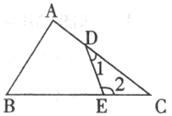
19.如图所示,△ABC中,D为AC上一点,E为BC上一点,若∠1=28°30′,则∠1+∠2+∠A+∠B=
20.如图表示一辆汽车行驶的速度和时间的图像,请你用语言描述汽车的行驶情况 。

21.已知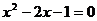 ,则
,则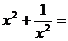 。
。
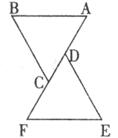
22.如下图,点C、D在AF上,AD=FC,AB=FE,要使△ABC≌△FED,还需填加条件 (填写一个即可)。
23.在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度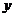 (厘米)与燃烧时间
(厘米)与燃烧时间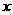 (小时)之间的关系如下图所示。请你根据图像所提供的信息回答下列问题:
(小时)之间的关系如下图所示。请你根据图像所提供的信息回答下列问题:
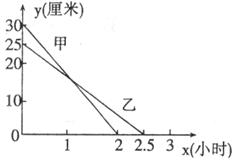
甲、乙两根蜡烛燃烧前的高度分别是 厘米、 厘米,从点燃到燃尽所用的时间分别是 小时、 小时。
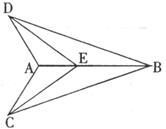
24.如下图,点E在AB上,AD=AC,∠DAB=∠CAB。写出图中所有全等三角形 。
25.某商店出售商品时,在进价的基础上又加了一定的利润,其数量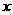 与售价
与售价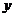 的关系如下表所示,那么售价
的关系如下表所示,那么售价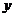 与的数量
与的数量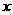 之间的关系式是 。
之间的关系式是 。
数量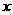 (千克)
(千克)
1
2
3
4
…
售价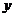 (元)
(元)
8+0.4
16+0.8
24+1.2
32+1.6
…
三、解答题:(每小题6分,满分12分)
26.下列各数都是由四舍五入法得到的近似数,它们分别精确到哪一位?各有几个有效数字?
(1)小红的体重为
(2)小明的妈妈的年薪约为5万元;
(3)月球轨道呈椭圆形,远地点平均距离为4.055×
27.下表是佳佳往小姨家打长途电话的几次收费标准记录:
时间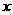 (分)
(分)
1
2
3
4
5
6
7
电话费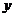 (元)
(元)
0.6
1.2
1.8
2.4
3.0
3.6
4.2
回答下列问题:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)帮助佳佳预测一下,如果她打电话用的时间是10分钟,那么需要付多少电话费;
(3)请你写出通话时间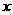 (分钟)(
(分钟)(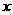 为正整数)与所要付的电话费
为正整数)与所要付的电话费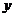 (元)之间的关系式。
(元)之间的关系式。
四、画图题:(28小题8分,29小题6分,满分14分)
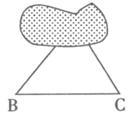
28.小明在练习本上画的△ABC被墨迹污染(如下图),请你帮助小明用尺规作一个与原来完全重合的△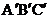 。要求:保留作图痕迹,不写作法,说明理由。
。要求:保留作图痕迹,不写作法,说明理由。
29.下图是把4×4的正方形方格图形沿方格线分割成两个全等图形,请在下列三个4×4的正方形方格中,沿方格线分别画出三种不同的分法,把图形分割成两个全等图形。


五、探索题:(满分10分)
30.如下图,△ABC中,∠ACB=90°,D为AB上一点,过D点作AB的垂线,交AC于E,交BC的延长线于F。
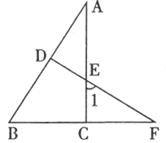
(1)∠1与∠B有什么关系?说明理由。
(2)若BC=BD,请你探索AB与FB的数量关系,并且说明理由。
六、实际应用题:(31小题8分,32小题11分,满分19分)
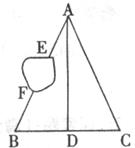
31.如图,A、B、C、D是四个村庄,B、D、C三村在一条东西走向公路的沿线上,且D村到B村、C村的距离相等;村庄A、C,A、D间也有公路相连,且公路AD是南北走向;只有村庄A、B之间由于间隔了一个小湖,所以无直接相连的公路。现决定在湖面上造一座斜拉桥,测得AC=
32.一天上午6点, (小时)的关系可用下列图中的折线表示。根据图中提供的信息,解答下列问题:
(小时)的关系可用下列图中的折线表示。根据图中提供的信息,解答下列问题:
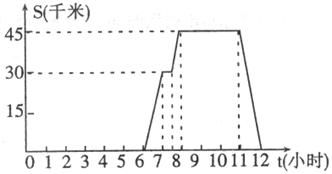
(1)开会地点离学校多远?
(2)
(3)请你用一段简短的话,对