2007-2008学年度烟台市莱州第二学期八年级期末质量检测
数学试卷
一、填空题(每小题3分,共30分)
1.方程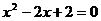 根的情况是 .
根的情况是 .
2.请写一个有两个相等实数根的一元二次方程 .
3.关于y的一元二次方程 的一根为2,则另一根为
.
的一根为2,则另一根为
.
4.若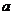 是方程
是方程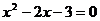 的一个根,则
的一个根,则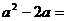 .
.
5.在Rt△ABC中,斜边AB上的高CD=
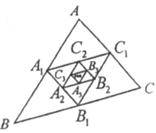
6.如图,已知△ABC的周长为1,分别连接AB,BC,CA各边的中点得△A1B
7.若函数 是反比例函数,则
是反比例函数,则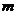 的值是
.
的值是
.
8.如图,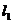 是反比例函数
是反比例函数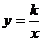 在第一象限内的图象,且过点(2,1),
在第一象限内的图象,且过点(2,1),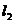 与
与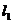 关于
关于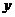 轴对称,那么图象
轴对称,那么图象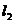 的函数表达式为
(
的函数表达式为
(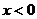 ).
).
9.反比例函数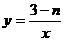 的图象在每个象限内,
的图象在每个象限内,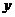 的值随
的值随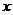 值的增大而增大,那么
值的增大而增大,那么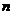 的取值范围是 .
的取值范围是 .
10.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E,F,AB=2,BC=3,则图中阴影部分的面积为 .

二、选择题(每小题3分,共30分)
11.下列方程中,是一元二次方程的是( )
A.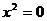 B.
B.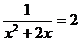
C.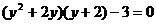 D.
D.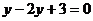
12.用配方法解一元二次方程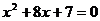 ,可将方程变形为( )
,可将方程变形为( )
A.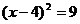 B.
B.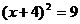
C. D.
D.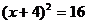
13.用反证法证明:在一个三角形中至少有一个内角小于或等于60°.证明过程中,可以先( )
A.假设三个内角没有一个小于60°的角
B.假设三个内角没有一个等于60°的角
C.假设三个内角没有一个小于或等于60°的角
D.假设三个内角没有一个大于或等于60°的角
14.绿茵场上,足球运动员将球踢出,球的飞行高度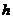 (米)与前行距离
(米)与前行距离 (米)之间的关系为:
(米)之间的关系为: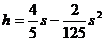 ,那么当足球落地时距离原来的位置有( )
,那么当足球落地时距离原来的位置有( )
A.
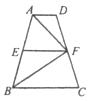
15.如图,在梯形ABCD中,AD//BC,中位线EF=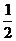 AB,下列结论:①EF=
AB,下列结论:①EF=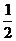 (AD+BC);②∠AFD+∠BFC=90°;③S△ABF=
(AD+BC);②∠AFD+∠BFC=90°;③S△ABF=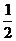 S梯形ABCD;④BF平分∠ABC.其中正确的有( )
S梯形ABCD;④BF平分∠ABC.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
A.1个 B.2个 C.3个 D.4个
16.关于反比例函数 ≠0)有下列说法:①图象在一、三象限;②图象在二、四象限;③
≠0)有下列说法:①图象在一、三象限;②图象在二、四象限;③ 的值随
的值随 值的增大而增大;④图象与坐标轴无交点.其中正确的说法有( )
值的增大而增大;④图象与坐标轴无交点.其中正确的说法有( )
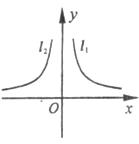
17.已知直线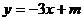 和双曲线
和双曲线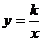 在直角坐标系中的位置如图所示,下列结论:①
在直角坐标系中的位置如图所示,下列结论:① ,②
,②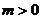 ,③
,③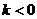 ,④
,④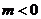 .其中正确的是( )
.其中正确的是( )
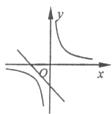
A.①② B.②③ C.③④ D.①④
18.书包里有数学书3本、英语书2本、语文书5本,从中任意抽取一本,是数学书的概率是( )
A.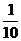 B.
B.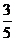 C.
C.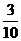 D.
D.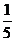
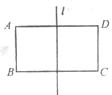
20.如图,在矩形ABCD中,AB=2,AD=2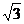 ,一条对称轴
,一条对称轴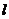 上有一动点P,当点P运动到某个位置时,可以和矩形顶点中的某两个连接构成等边三角形.满足上述条件的点P的位置有( )
上有一动点P,当点P运动到某个位置时,可以和矩形顶点中的某两个连接构成等边三角形.满足上述条件的点P的位置有( )
A.2个 B.4个 C.5个 D.6个
三、解答题(本大题共8个小题,满分60分.解答题要写出必要的文字说明或说理过程或演算步骤)
21.(满分5)尺规作图
利用直尺和圆规作出一个30°的角.
要求:写出作法,保留作图痕迹,但不需要证明.
22.(满分10分)
已知: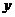 与
与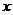 成反比例,并且当
成反比例,并且当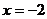 时,
时,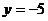 .
.
(1)求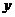 与
与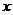 之间的函数关系式;
之间的函数关系式;
(2)直线 与(1)中所求函数图象交点的横坐标是l,试求
与(1)中所求函数图象交点的横坐标是l,试求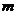 的值;
的值;
(3)在(2)中,是否还有另外的交点?若有,请直接写出交点的坐标.
23.(满分6分)
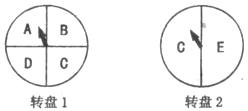
元旦联欢会上,小明设计了一个游戏:游戏者分别转动如图的两个可以自由转动的转盘各一次,当两个转盘的指针所指字母相同时,他就可以获得一次指定一位到会者为大家表演节目的机会.
(1)利用树状图或列表的方法(只选其中一种)表示出游戏可能出现的所有结果;
(2)若小亮参加一次游戏,则他能获得这种指定机会的概率是多少?
24.(满分5分)
已知:关于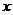 的一元二次方程
的一元二次方程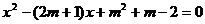 .
.
求证:不论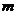 取何值,方程总有两个不相等的实数根;
取何值,方程总有两个不相等的实数根;
25.(满分8分)
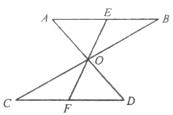
如图,AD、BC交于点O,EF过点O分别交AB、CD于点E、F.OA=OD,OE=OF.
(1)求证:AB=CD
(2)在图中,连接某些线段可以构成一个平行四边形,请你将可以构成的平行四边形一一列举出来(不需要证明).
26.(满分7分)
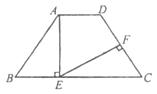
如图,在等腰梯形ABCD中,AD//BC,AB=CD,∠B=60°.AE⊥BC于E;EF⊥CD于F,点F是CD的中点.求证:AD=BE.
27.(满分9分)
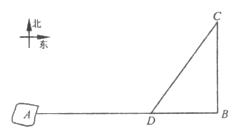
小岛A在码头B的正西方向,A、B相距40海里.上午9点,一渔船和一游艇同时出发,渔船以20海里/时的速度从B码头向正北出海作业,游艇以25海里/时的速度从A岛返回B码头.一段时间后,渔船因故障停航在C处并发出讯号.游艇在D处收到讯号后直接向渔船驶去,上午11点到达C处.游艇在上午几点收到讯号?
28.(满分l0分)
公园的风景墙上设计了一种矩形窗户(如图1),在矩形窗框内有等宽的四边形窗格(空白处用以通风透光).图2是其设计图,已知AD=
