2007-2008学年度临沂市莒南上学期阶段性质量检测
八年级数学试题
一、选择题:(每小题3分,共30分)将唯一正确答案的代号字母填在下面的方格内.
1.函数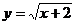 的自变量
的自变量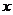 的取值范围是:
的取值范围是:
A.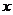 ≥一2 B.
≥一2 B.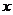 <一
<一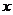 >一2 D.
>一2 D.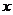 ≤一2
≤一2
2.点P1(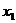 ,
,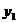 ),P2(
),P2(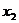 ,
,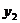 )是一次函数
)是一次函数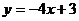 图象上的两个点,且
图象上的两个点,且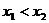 ,则
,则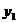 与
与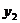 的大小关系是:
的大小关系是:
A.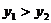 B.
B.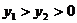
C.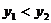 D.
D.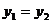
3.已知一次函数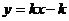 ,若
,若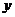 随着
随着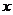 的增大而减小,则该函数图象经过:
的增大而减小,则该函数图象经过:
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
4.将直线y=2x向右平移两个单位,所得的直线是:
A.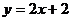 B.
B.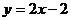
C.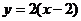 D.
D.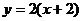
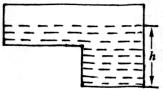
5.如图是某蓄水池的横截面示意图,分为深水池和浅水池,如果这个蓄水池以固定的速度往里注水,下面能大致表示水的最大深度h与时间t之间的关系的图象是:
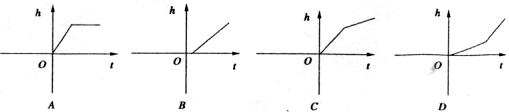
6.要清楚地表示病人一天的体温变化情况,应选用:
A.扇形统计图 B.条形统计图
C.折线统计图 D.以上都不对
7.如图是学生会体育部长调查了本年级喜欢排球、篮球、足球的人数并画出了条形图,从图中得到下述结论:①可以直接看出喜欢各类球的具体人数;②可以直接看出喜欢篮球的人数最多③可以直接看出喜欢各类球的人数的百分比;④可以直接看出喜欢各类球人数的变化情况.其中正确的是:
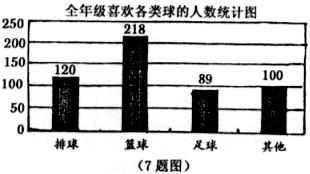
A.①④ B.①② C.①②④ D.①②③④
8.如图,AD平分∠BAC,AB=AC,连接BD、CD并延长交AC于点F、AB于点E,则图中全等三角形的对数是:
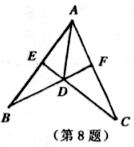
A.2 B.
9.在△ABC和△DEF中,已知∠A=∠D,∠B=∠E,要判定这两个三角形全等,还需要条件:
A.AB=ED B.AB=FD C.AC=FD D.∠A=∠F
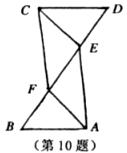
10.如图,△ABF≌△CDE,则①AB//CD;②BE=DF;③△AEF≌CFE;④AE//CF.这四个必成立的是:
A.① B.①② C.①②③ D.①②③④
11.如果直线 经过第一、二、三象限,那么
经过第一、二、三象限,那么 ____________0(填“>”、“<”、“=”)
____________0(填“>”、“<”、“=”)
12.在平面直角坐标系中,直线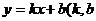 为常数且
为常数且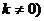 可以看作直线
可以看作直线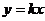 沿
沿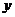 轴向____________平移___________ 个单位长度而得到。
轴向____________平移___________ 个单位长度而得到。
13.若一次函数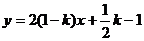 的图象不过第一象限,则
的图象不过第一象限,则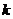 的取值范围为___________。
的取值范围为___________。
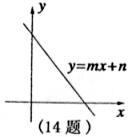
14.直线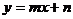 如图所示,化简:
如图所示,化简: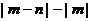 =______________。
=______________。
15.直线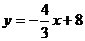 与
与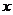 轴、
轴、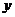 轴分别交于点A和点B,M是OB的中点,则△AOM的面积为________。
轴分别交于点A和点B,M是OB的中点,则△AOM的面积为________。
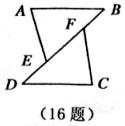
16.如图,点D、E、F、B在同一直线上,AB//CD,AE//CF,且AE=CF,若BD=10,BF=2,则EF=_________________。
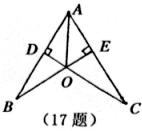
17.如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD交于点O,且OD=OE,若∠DAO=30°,则∠B=__________。
18.在Rt△ABC中,∠C=90°,BD平分∠ABC,若CD=
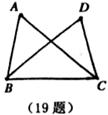
19.如图,AB=DC,要使△ABC≌△DCB,只需增加一个条件是_____________________.(只填一个你认为适合的条件)
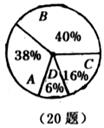
20.某校八年级(3)班有50名同学,综合数值评价“运动与健康”方面的等级统计如图所示,则该班“运动与健康”评价等级为A的人数是________________________________________。
三、解答题:(共55分)
21.一次函数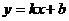 经过点A(3,一2)和点B,其中点B是直线
经过点A(3,一2)和点B,其中点B是直线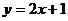 和
和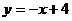 的交点,求这个一次函数解析式.(7分)
的交点,求这个一次函数解析式.(7分)
22.图为某班学生外出乘车、步行、骑车的人数分布直方图和扇形统计图。
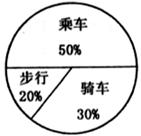
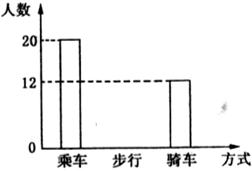
(1)该班有多少名学生?
(2)补上分布直方图中步行的空缺部分:
(3)在扇形统计图中,求骑车人数所占的圆心角度数;
(4)若全年级有500人,估计该年级步行人数.(8分)
23.如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且DB=DC.试讨论与∠EBD相等的角是哪个角?并加以证明.(8分)
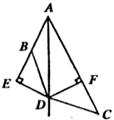
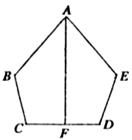
24.如图,AB=AE,BC=ED,∠ABC=∠AED,点F是CD的中点.
(1)求证:AF⊥CD;
(2)你连接BE后,设AF与BE的交点为O,你还能得出什么新的结论?请写出三个(不要证明,但必须与B、E有关).(10分)
25.某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为6000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%,乙商场的优惠条件是:每台优惠20%.
(1)在什么情况下到甲商场购买合算?
(2)在什么情况下到乙商场购买合算?
(3)在什么情况下到甲、乙两商场购买花钱一样多?(10分)
26.光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,现将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见下表:
每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800元
1600元
B地区
1600元
1200元
(1)设派往A地区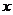 台Z型联合收割机,租赁公司这50台联合收割机一天获得的租金为
台Z型联合收割机,租赁公司这50台联合收割机一天获得的租金为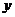 (元),求
(元),求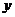 与
与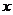 之间的函数关系式,并写出
之间的函数关系式,并写出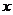 的取值范围;
的取值范围;
(2)如果农机租赁公司这50台收割机一天获得的租金总额不低于79600元,说明有多少种分派方案?
(3)哪种方案获得的租金最多?(12分)