2008年内江市初中毕业会考暨高中阶段招生考试
数学试卷
会考卷(共100分)
第Ⅰ卷(选择题 共36分)
一、选择题:(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.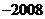 的绝对值是(
)
的绝对值是(
)
A.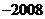 B.
B. C.
C.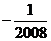 D.
D.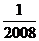
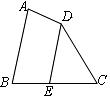
2.如图,在四边形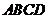 中,点
中,点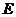 在
在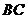 上,
上,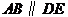 ,
,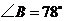 ,
,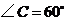 ,则
,则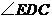 的度数为( )
的度数为( )
A.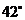 B.
B.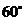 C.
C.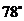 D.
D.
3.下列图形中,既是中心对称图形又是轴对称图形的是( )
A.等边三角形 B.平行四边形 C.抛物线 D.双曲线
4.下列调查方式中适合的是( )
A.要了解一批节能灯的使用寿命,采用普查方式
B.调查你所在班级同学的身高,采用抽样调查方式
C.环保部门调查沱江某段水域的水质情况,采用抽样调查方式
D.调查全市中学生每天的就寝时间,采用普查方式
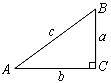
5.如图,在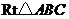 中,
中,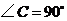 ,三边分别为
,三边分别为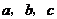 ,则
,则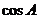 等于( )
等于( )
A.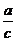 B.
B.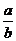 C.
C.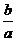 D.
D.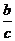
6.函数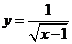 的自变量
的自变量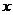 的取值范围在数轴上可表示为(
)
的取值范围在数轴上可表示为(
)

7.某班七个兴趣小组人数分别为:3,3,4,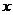 ,5,5,6,已知这组数据的平均数是4,则这组数据的中位数是(
)
,5,5,6,已知这组数据的平均数是4,则这组数据的中位数是(
)
A.2 B.
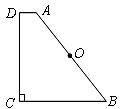
8.如图,在直角梯形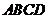 中,
中,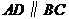 ,
,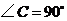 ,且
,且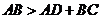 ,
,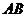 是
是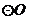 的直径,则直线
的直径,则直线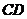 与
与 的位置关系为(
)
的位置关系为(
)
A.相离 B.相切 C.相交 D.无法确定
9.若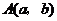 ,
,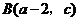 两点均在函数
两点均在函数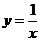 的图象上,且
的图象上,且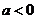 ,则
,则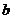 与
与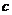 的大小关系为(
)
的大小关系为(
)
A.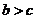 B.
B.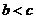 C.
C.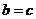 D.无法判断
D.无法判断
10.如图所示,同时自由转动两个转盘,指针落在每一个数上的机会均等,转盘停止后,两个指针同时落在奇数上的概率是( )

A.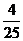 B.
B.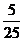 C.
C.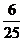 D.
D.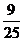
11.在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来.如图所示,则这堆正方体货箱共有( )
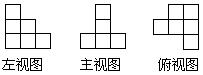
A.9箱 B.10箱 C.11箱 D.12箱
12.下列命题中,真命题的个数为( )
①对角线互相垂直平分且相等的四边形是正方形
②如果四边形的两条对角线互相垂直,那么它的面积等于两条对角线长的积的一半
③在一个圆中,如果弦相等,那么所对的圆周角相等
④已知两圆半径分别为5,3,圆心距为2,那么两圆内切
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题 共64分)
二、填空题(本大题共4小题,每小题5分,共20分.请将最后答案直接填在题中横线上.)
13.分解因式: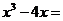 .
.
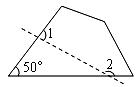
14.在如图所示的四边形中,若去掉一个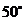 的角得到一个五边形,则
的角得到一个五边形,则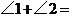 度.
度.
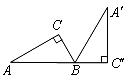
15.如图,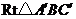 是由
是由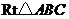 绕
绕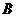 点顺时针旋转而得,且点
点顺时针旋转而得,且点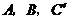 在同一条直线上,在
在同一条直线上,在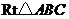 中,若
中,若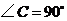 ,
,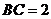 ,
,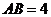 ,则斜边
,则斜边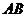 旋转到
旋转到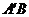 所扫过的扇形面积为
.
所扫过的扇形面积为
.
16.根据图中数字的规律,在最后一个图形中填空.

三、解答题(本大题共5个小题,共44分.解答题必须写出必要的文字说明、证明过程或推演步骤.)
17.(8分)计算: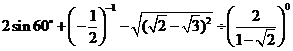
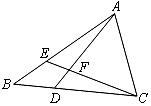
18.(9分)如图,在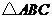 中,点
中,点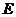 在
在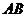 上,点
上,点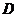 在
在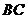 上,
上,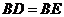 ,
,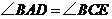 ,
,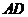 与
与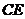 相交于点
相交于点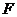 ,试判断
,试判断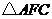 的形状,并说明理由.
的形状,并说明理由.
19.(9分)某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为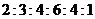 .第三组的频数是12.请你回答:
.第三组的频数是12.请你回答:

(1)本次活动共有 件作品参赛;
(2)上交作品最多的组有作品 件;
(3)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?
(4)对参赛的每一件作品进行编号并制作成背面完全一致的卡片,背面朝上的放置,随机抽出一张卡片,抽到第四组作品的概率是多少?
20.(9分)今年以来受各种因素的影响,猪肉的市场价格仍在不断上升.据调查,今年5月份一级猪肉的价格是1月份猪肉价格的1.25倍.小英同学的妈妈同样用20元钱在5月份购得一级猪肉比在1月份购得的一级猪肉少0.4斤,那么今年1月份的一级猪肉每斤是多少元?
(1)求反比例函数的解析式;
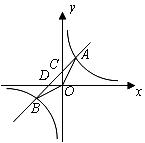
21.(9分)如图,一次函数 的图象经过第一、二、三象限,且与反比例函数图象相交于
的图象经过第一、二、三象限,且与反比例函数图象相交于 两点,与
两点,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,
, .且点
.且点 横坐标是点
横坐标是点 纵坐标的2倍.
纵坐标的2倍.
(2)设点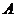 横坐标为
横坐标为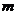 ,
,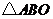 面积为
面积为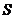 ,求
,求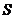 与
与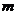 的函数关系式,并求出自变量的取值范围.
的函数关系式,并求出自变量的取值范围.
加试卷(共50分)
一、填空题(本大题共4小题,每小题5分,共20分.请将最简答案直接填在题中横线上)
1.有甲、乙、丙三种商品,如果购甲3件、乙2件,丙1件共需315元钱,购甲1件、乙2件、丙3件共需285元钱,那么购甲、乙、丙三种商品各一件共需 元钱.
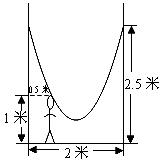
2.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
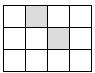
3.如图,在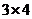 的矩形方格图中,不包含阴影部分的矩形个数是
个.
的矩形方格图中,不包含阴影部分的矩形个数是
个.
4.如图,当四边形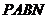 的周长最小时,
的周长最小时,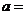 .
.
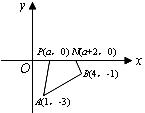
二、解答题(本大题共3个小题,每小题10分,共30分.解答题必须写出必要的文字说明、证明过程或推演步骤.)
例如:考查代数式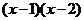 的值与0的大小
的值与0的大小
当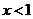 时,
时,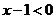 ,
,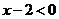 ,
,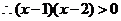
当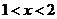 时,
时,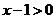 ,
,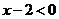 ,
,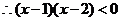
当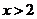 时,
时,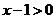 ,
,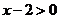 ,
,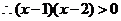
综上:当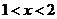 时,
时,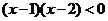
当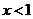 或
或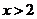 时,
时,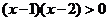
(1)
填写下表:(用“ ”或“
”或“ ”填入空格处)
”填入空格处)
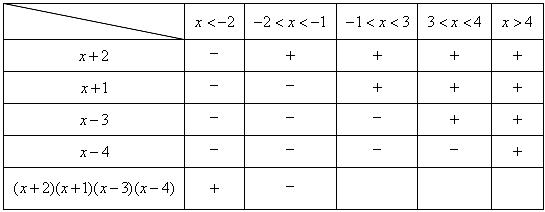
(2)由上表可知,当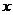 满足
时,
满足
时, ;
;
(3)运用你发现的规律,直接写出当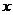 满足 时,
满足 时,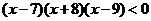 .
.
6.(10分)“5.12”汶川大地震后,某药业生产厂家为支援灾区人民,准备捐赠320箱某种急需药品,该厂家备有多辆甲、乙两种型号的货车,如果单独用甲型号车若干辆,则装满每车后还余20箱未装;如果单独用同样辆数的乙型号车装,则装完后还可以再装30箱,已知装满时,每辆甲型号车比乙型号车少装10箱.
(1)求甲、乙两型号车每辆车装满时,各能装多少箱药品?
(2)已知将这批药品从厂家运到灾区,甲、乙两型号车的运输成本分别为320元/辆和350元/辆.设派出甲型号车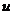 辆,乙型号车
辆,乙型号车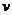 辆时,运输的总成本为
辆时,运输的总成本为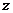 元,请你提出一个派车方案,保证320箱药品装完,且运输总成本
元,请你提出一个派车方案,保证320箱药品装完,且运输总成本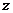 最低,并求出这个最低运输成本为多少元?
最低,并求出这个最低运输成本为多少元?
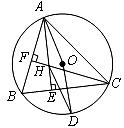
7.(10分)如图,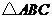 内接于⊙
内接于⊙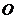 ,
,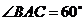 ,点
,点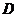 是的中点.
是的中点.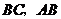 边上的高
边上的高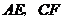 相交于点
相交于点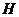 .
.
试证明:
(1)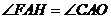 ;
;
(2)四边形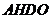 是菱形.
是菱形.