1．哈市4月份某天的最高气温是5℃，最低气温是－3℃，那么这天的温差（最高气温减最低气温）是（    ）．

  （A）－2℃         （B） 8℃           （C）一8℃          （D） 2℃

2．下列运算中，正确的是（    ）．

  （A）x²＋x²＝x⁴       （B）x²÷x＝x²       （C）x³－x²＝x       （D）x?x²＝x³

3．在下列图形中，既是轴对称图形又是中心对称图形的是（      ）．

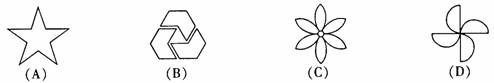
4．下图是某一几何体的三视图，则这个几何体是（      ）。

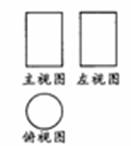
   （A）圆柱体           （B）圆锥体              

   （C）正方体           （D）球体

5．9的平方根是（    ）．

   （A）3         （B）±3         （C）一3         （D）81

6．某商店出售下列四种形状的地砖：①正三角形；②正方形；③正五边形；④正六边形。若只选购其中一种地砖镶嵌地面，可供选择的地砖共有（     ）．

（A）4种       （B）3种         （C）2种         （D）1种

7．如图，圆锥形烟囱帽的底面直径为80cm，母线长为50cm，则这样的烟囱帽的侧面积是（    ）．

（A）4000πcm²     （B）3600πcm²

（C）2000πcm²     （D）1000πcm²

 （A）k＞2        （B） k≥2            （C）k≤2            （D） k＜2

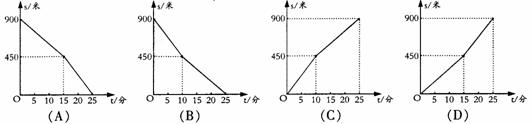
9．小亮每天从家去学校上学行走的路程为900米，某天他从家去上学时以每分30米的速度行走了450米，为了不迟到他加快了速度，以每分45米的速度行走完剩下的路程，那么小亮行走过的路程S（米）与他行走的时间t（分）之间的函数关系用图象表示正确的是（     ）．

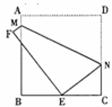
10．如图，将边长为8cm的正方形纸片ABCD折叠，使点D落在BC边中点E处，点A落在点F处，折痕为MN，则线段CN的长是（    ）．

    （A）3cm         （B）4cm

    （C）5cm         （D）6cm

第Ⅱ卷 非选择题（共90分）

（16、*16任选一题）

11．太阳的半径约是69660千米，用科学记数法表示（保留3个有效数字）约是      千米．

12．函数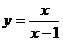的自变量x的取值范围是           ．

13．把多项式2mx²－4mxy＋2my²分解因式的结果是                       ．

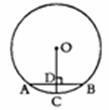
14．如图，AB为⊙O的弦，⊙O的半径为5，OC⊥AB于点D，交⊙O于点C，且CD＝l，则弦AB的长是             ．

15．一个袋子中装有6个球，其中4个黑球2个白球，这些球除颜色外，形状、大小、质地等完全相同．搅匀后，在看不到球的条件下，随机从这个袋子中摸出一个球为白球的概率是           ．

16．2008年7月1日是星期二，那么2008年7月16日是星期          ．

*16．若x＝1是一元二次方程x²＋x＋c＝0的一个解，则c²＝        ．

17．观察下列图形：

它们是按一定规律排列的，依照此规律，第20个图形共有         个★．

18．已知菱形ABCD的边长是6，点E在直线AD上，DE＝3，连接BE与对角线AC相交于点M，则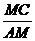的值是                 。

19．（本题 5分）

   先化简，再求代数式的值，其中x＝4sin45°－2cos60°

 20．（本题5分）

   △ABC在平面直角坐标系中的位置如图所示．

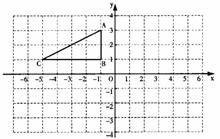
    （1）将△ABC向右平移6个单位得到△A₁B₁C₁，请画出△A₁B₁C₁；并写出点C₁的坐标；

（2）将△ABC绕原点O旋转180°得到△A₂B₂C₂，请画出△A₂B₂C₂。

21．（本题5分）

小李想用篱笆围成一个周长为60米的矩形场地，矩形面积S（单位：平方米）随矩形一边长x（单位：米）的变化而变化．

（1）求S与x之间的函数关系式，并写出自变量x的取值范围；

（2）当x是多少时，矩形场地面积S最大？最大面积是多少？

（参考公式：二次函数y＝ax²＋bx＋c＝0，当x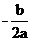＝时，）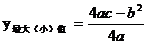

22．（本题5分

已知：如图，B、E、F、C四点在同一条直线上，AB＝DC，BE＝CF，∠B＝∠C．

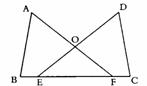
求证：OA＝OD．

23．（本题 6分）

如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处．求此时轮船所在的B处与灯塔P的距离（结果保留根号）．

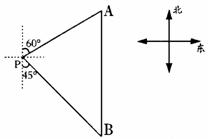
24．（本题6分）

哈市某中学为了解该校学生对四种国家一级保护动物的喜爱情况，围绕“在丹顶鹤、大熊猫、滇金丝猴、藏羚羊四种国家一级保护动物中，你最喜欢哪一种动物？（只写一种）”这一问题，在全校范围内随机抽取部分同学进行问卷调查．甲同学根据调查结果计算得知：最喜欢丹顶鹤的学生人数占被抽取人数的16％；乙同学根据调查结果绘制成如下不完整的

条形统计图．请你根据甲、乙两位同学提供的信息解答下列问题：

（1）在这次调查中，一共抽取了多少名学生？

（2）补全条形统计图的空缺部分；

（3）如果全校有1200名学生，请你估计全校最喜欢滇金丝猴的学生有多少名？

25．（本题6分）

如图所示，有两种形状不同的直角三角形纸片各两块，其中一种纸片的两条直角边长分别为1和2，另一种纸片的两条直角边长都为2．图a、图b、图c是三张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1．请用三种方法将图中所给四块直角三角形纸片拼成平行四边形（非矩形），每种方法要把图中所给的四块直角三角形纸片全部用上，互不重叠且不留空隙，三种方法所拼得的平行四边形（非矩形）的周长互不相等，并把你所拼得的图形按实际大小画在图a、图b、图c的方格纸上。

 要求：（l）所画图形各顶点必须与方格纸中的小正方形顶点重合。

      （2）画图时，要保留四块直角三角形纸片的拼接痕迹。

26．（本题8分）

荣昌公司要将本公司100吨货物运往某地销售，经与春晨运输公司协商，计划租用甲、乙两种型号的汽车共6辆，用这6辆汽车一次将货物全部运走，其中每辆甲型汽车最多能装该种货物16吨，每辆乙型汽车最多能装该种货物18吨．已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元；租用2辆甲型汽车和1辆乙型汽车共需费用2450元，且同一种型号汽车每辆租车费用相同．

（1）求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元？

（2）若荣昌公司计划此次租车费用不超过5000元．通过计算求出该公司有几种租车方案？请你设计出来,并求出最低的租车费用．

27．（本题10分）

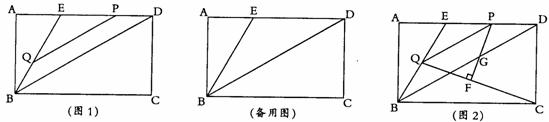
在矩形ABCD中，点E是AD边上一点，连接BE，且∠ABE＝30°，BE＝DE，连接BD．点P从点E出发沿射线ED运动，过点P作PQ∥BD交直线BE于点Q．

(1) 当点P在线段ED上时（如图1），求证：BE＝PD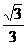＋PQ；

 （2）若 BC＝6，设PQ长为x，以P、Q、D三点为顶点所构成的三角形面积为y，求y与 x的函数关系式（不要求写出自变量x的取值范围）；

（3）在②的条件下，当点P运动到线段ED的中点时，连接QC，过点P作PF⊥QC，垂足为F，PF交对角线BD于点G（如图2），求线段PG的长。

28．（本题10分）

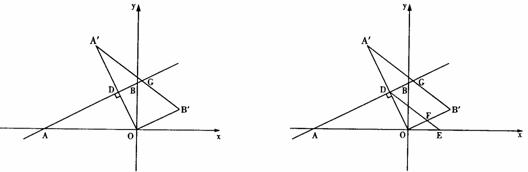
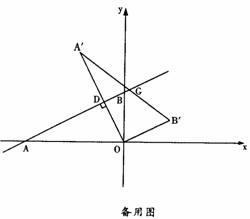
如图，在平面直角坐标系中，直线y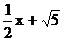＝与x轴、y轴分别交于A、B两点，将△ABO绕原点O顺时针旋转得到△A´B´O，并使OA´⊥AB，垂足为D，直线AB与线段A´B´相交于点G．动点E从原点O出发，以1个单位/秒的速度沿x轴正方向运动，设动点E运动的时间为t秒．

（1）求点D的坐标；

（2）连接DE，当DE与线段OB´相交，交点为F，且四边形DFB´G是平行四边形时，（如图2）求此时线段DE所在的直线的解析式；

（3）若以动点为E圆心，以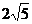为半径作⊙E，连接A´E，t为何值时。Tan∠EA´B´＝？并判断此时直线A´O与⊙E的位置关系，请说明理由。