2008年山东省淄博市中等学校招生考试
数学试卷
第Ⅰ卷(选择题 共36分)
一、选择题:本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项涂在答题卡的相应位置上。每小题3分,错选、不选、选出的答案超过一个,均记0分。
1.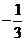 的相反数是
的相反数是
A. 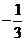 B.
B. 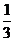
 C. 3 D. -3
C. 3 D. -3
2.下列运算正确的是
A.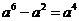 B.
B.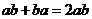 C.
C.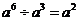 D.
D. 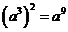
3.如图,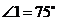 ,要使a∥b,则∠2等于
,要使a∥b,则∠2等于
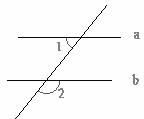
A.75° B.95° C.105° D.115°
4.与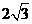 是同类二次根式的是
是同类二次根式的是
A.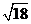 B.
B.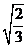 C.
C.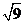 D.-
D.-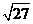
5.如图,在RT△ABC中,tanB=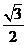 ,BC=
,BC=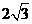 ,则AC等于
,则AC等于
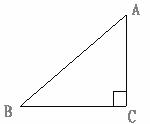
A. 3 B. 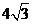 D.6
D.6
6.下面是四位同学对他们学习小组将要共同进行的一次统计活动分别设计的活动程序,其中正确的是
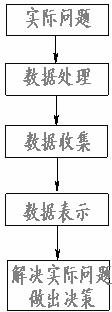
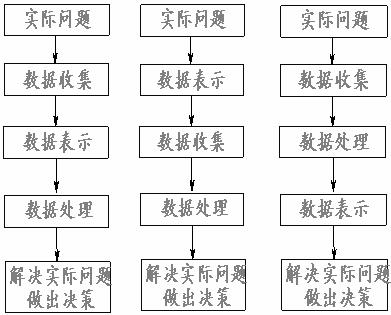
A. B. C. D.
7.已知点(-2,y1),(-1,y2),(3,y3),和(-3,-2)都在反比例函数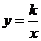 的图象上,那么y1,y2 ,与y3的大小关系是
的图象上,那么y1,y2 ,与y3的大小关系是
A.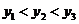
 B.
B.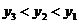 C.
C.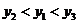 D.
D.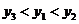
8.如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点。在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有
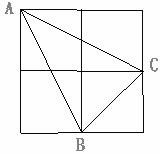
A.1个 B.2个 C.3个 D.4个
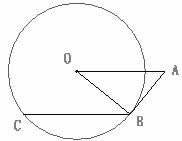
9.如图,A是半径为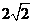 的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦
的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦
BC∥OA,则BC的长为
A. 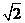
 B.
B. 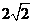 D.4
D.4
10.小红设计了一个计算程序,并按此程序进行了两次计算。在计算中输入了不同的x值,
但一次没有结果,另一次输出的结果是42,则这两次输入的x值不可能是
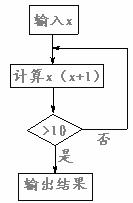
A. 0,2 B. -1,-
11.如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标分别变成原来的2倍,得到点A′,B′,C′。下列说法正确的是
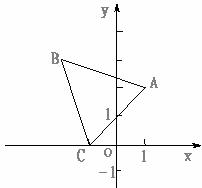
A.△A′B′C′与△ABC是位似图形,位似中心是点(1,0)
B.△A′B′C′与△ABC是位似图形,位似中心是点(0,0)
C.△A′B′C′与△ABC是相似图形,但不是位似图形
D.△A′B′C′与△ABC不是相似图形
12.观察下面几组数:
1,3,5,7,9,11,13,15,……
2,5,8,11,14,17,20,23,……
7,13,19,25,31,37,43,49,……
这三组数具有共同的特点。
现在有上述特点的一组数,第一个数是3,第三个数是11,则其第n个数为
A.8-5 B.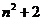
 C. 4n-1 D.
C. 4n-1 D.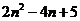
第Ⅱ卷 (菲选择题 共84分)
二、填空题:本题共5小题,满分20分。只要求填写最后结果,每小题填对得4分。
13.若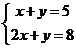 则x+2y=_________________.
则x+2y=_________________.
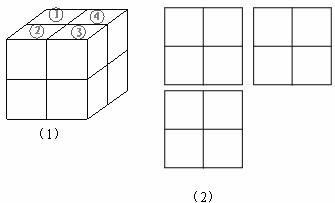
14.如图(1),用八个同样大小的小立方体搭成一个大立方体,小明从上面的四个小立方体中取走了两个后,得到的新几何体的三视图如图(2)所示,则他拿走的两个小立方体的序号是_________________________.(只填写满足条件的一种情况即可)
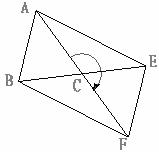
15.如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF。当∠ACB为________________度时,四边形ABFE为矩形。
16.在-9,-6,-3,-1,2,3,6,8,11这九个数中,任取一个作为a值,能够使关
于x的一元二次方程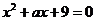 有两个不相等的实数根的概率是_______________.
有两个不相等的实数根的概率是_______________.
17.关于x的不等式组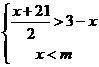 的所有整数解的和是-7,则m的取值范围是___
的所有整数解的和是-7,则m的取值范围是___
________________________________.
三、解答题:本大题共8小题,共64分。解答要写出必要的文字说明、证明过程或演算步骤。
18.(本题满分6分)
计算: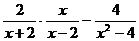
19.(本体满分6分)
已知:如图,AD与BC相交于点O,∠CAB=∠DBA,AC=BD,求证:
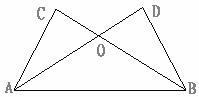
(1)∠C=∠D;
(2)△AOC≌△BOD.
20.(本题满分8分)
2007年底,某校初四年级一班的同学曾经到学校附近的农贸市场调查了这个市场里100家商户中的10家。这10家商户平均每天送出的超薄塑料购物袋数量分别为(单位:把):
4 5 3 8 5 7 5 6 3 4
(1)请分别写出这组数据的众数、中位数;
(2)如果要选择一种统计图来表示这10家商户送出的超薄塑料购物袋的情况,在条形统计图、折线统计图、扇形统计图中你会选择哪一个?
(3)已知一把超薄塑料购物袋有50个。通过对样本的计算,估计该农贸市场一年要送出多少个超薄塑料购物袋(一年按350个营业日计算)?结果用科学记数法表示。
21.(本题满分8分)
把长为
22.(本题满分8分)
如图,AB是⊙O的直径,∠BAC的平分线AQ交BC于点P,交⊙O于点Q.已知AC=6,∠AQC=30°
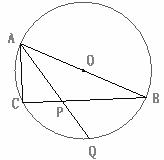
(1)求AB的长;
(2)求点P到AB的距离;
(3)求PQ的长。
23.(本题满分8分)
甲、乙两个仓库要向A、B两地调运小麦,已知甲库可以调出80吨,乙库可以调出40吨。A地需要小麦50吨,B地需要小麦70吨。甲、乙两库运往A、B地的费用如下表:
A地(元/吨)
B地(元/吨)
甲库
10
40
乙库
20
30
(1)设甲库运往A地x吨,求总运费y(单位:元)与x之间的函数关系式;
(2)那种方案总运费最省?哪种方案总运费最多?并求最省和最多的运费。
24.(本题满分10分)
一条抛物线经过点O与A(4,0)点,顶点B在直线y=kx+2k(k≠0)上。将这条抛物线先向上平移m(m>0)个单位,再向右平移m个单位,得到的抛物线的顶点仍然落在直线y=kx+2k上,点A移动到了点A′.
(1) 求K值及抛物线的表达式;
(2) 求使△A′OB′的面积是6032的m值。
25.(本题满分10分)
正方形ABCD的对角线交点为O,两条对角线把它分成了四个面积相等的三角形。
(1)平行四边形ABCD的两条对角线交点为O,若△AOB,△BOC,△COD,△DOA面积分别为S1,S2,S3,S4,试判断S1,S2,S3,S4的关系,并加以证明;
(2)四边形ABCD的两条对角线互相垂直,交点为O,若△AOB,△BOC,△COD,△DOA面积分别为S1,S2,S3,S4,试判断S1,S2,S3,S4的关系,并加以证明;
(3)四边形ABCD的两条对角线交点为O,若△AOB,△BOC,△COD,△DOA面积分别为S1,S2,S3,S4,试判断S1,S2,S3,S4的关系,并加以证明;
(4)四边形ABCD的两条对角线相等,交点为O,∠BAC=∠BDC,若△AOB,△BOC,△COD,△DOA面积分别为S1,S2,S3,S4,试只用S1,S3或只用S2,S4表示四边形ABCD的面积S.