2008年甘肃省兰州市初中毕业生学业考试
数学试卷(A)
一、选择题(本题共12个小题,每小题4分,共计48分.在每小题给出的4个选项中,只有一项是符合题目要求的)
1.如图是北京奥运会自行车比赛项目标志,则图中两轮所在圆的位置关系是( )

A.内含 B.相交 C.相切 D.外离
2.方程 的解是( )
的解是( )
A. B.
B. C.
C. 或
或 D.
D.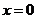
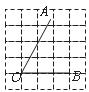
3.正方形网格中,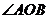 如图放置,则
如图放置,则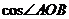 的值为( )
的值为( )
A.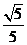 B.
B.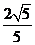 C.
C.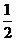 D.2
D.2
4.桌面上放着1个长方体和1个圆柱体,按下图所示的方式摆放在一起,其左视图是( )
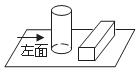

5.若反比例函数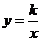 的图象经过点
的图象经过点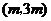 ,其中
,其中 ,则此反比例函数的图象在( )
,则此反比例函数的图象在( )
A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象限
6.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其它完全相同.小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( )
A.24 B.
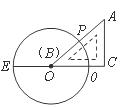
7.如图,已知 是⊙
是⊙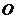 的直径,把
的直径,把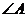 为
为 的直角三角板
的直角三角板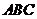 的一条直角边
的一条直角边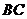 放在直线
放在直线 上,斜边
上,斜边 与⊙
与⊙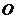 交于点
交于点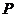 ,点
,点 与点
与点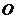 重合.将三角板
重合.将三角板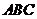 沿
沿 方向平移,使得点
方向平移,使得点 与点
与点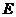 重合为止.设
重合为止.设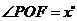 ,则
,则 的取值范围是(
)
的取值范围是(
)
A.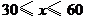 B.
B.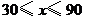
C.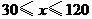 D.
D.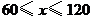
8.如图,现有一个圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( )
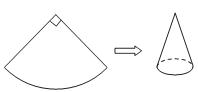
A.4cm B.3cm C.2cm D.1cm
9.已知二次函数 (
( )的图象如图所示,有下列4个结论:①
)的图象如图所示,有下列4个结论:①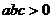 ;②
;②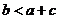 ;③
;③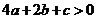 ;④
;④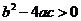 ;其中正确的结论有(
)
;其中正确的结论有(
)

A.1个 B.2个 C.3个 D.4个
10.下列表格是二次函数 的自变量
的自变量 与函数值
与函数值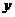 的对应值,判断方程
的对应值,判断方程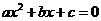 (
(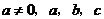 为常数)的一个解
为常数)的一个解 的范围是( )
的范围是( )

6.17
6.18
6.19
6.20





A. B.
B.
C. D.
D.
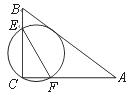
11.如图,在 中,
中, ,经过点
,经过点 且与边
且与边 相切的动圆与
相切的动圆与 分别相交于点
分别相交于点 ,则线段
,则线段 长度的最小值是(
)
长度的最小值是(
)
A. B.
B. C.5 D.48
C.5 D.48
12.把长为8cm的矩形按虚线对折,按图中的虚线剪出一个直角梯形,拆开得到一个等腰梯形,剪掉部分的面积为6cm2,则打开后梯形的周长是( )

A.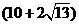 cm B.
cm B.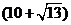 cm C.22cm D.18cm
cm C.22cm D.18cm
二、填空题(本题共8个小题,每小题4分,共32分,请把答案填在题中的横线上.)
13.函数 的自变量
的自变量 的取值范围为 .
的取值范围为 .
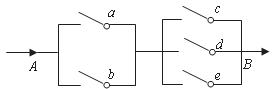
14.如图所示,有一电路 是由图示的开关控制,闭合a,b,c,d,e五个开关中的任意两个开关,使电路形成通路.则使电路形成通路的概率是 .
是由图示的开关控制,闭合a,b,c,d,e五个开关中的任意两个开关,使电路形成通路.则使电路形成通路的概率是 .
15.在同一坐标平面内,下列4个函数①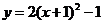 ,②
,②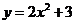 ,③
,③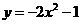 ,④
,④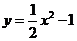 的图象不可能由函数
的图象不可能由函数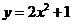 的图象通过平移变换、轴对称变换得到的函数是 (填序号).
的图象通过平移变换、轴对称变换得到的函数是 (填序号).
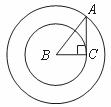
16.如图,在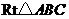 中,
中,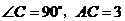 .将其绕
.将其绕 点顺时针旋转一周,则分别以
点顺时针旋转一周,则分别以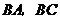 为半径的圆形成一圆环.则该圆环的面积为
.
为半径的圆形成一圆环.则该圆环的面积为
.
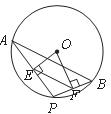
17.如图,点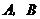 是⊙
是⊙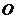 上两点,
上两点, ,点
,点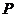 是⊙
是⊙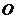 上的动点(
上的动点(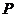 与
与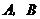 不重合)连结
不重合)连结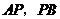 ,过点
,过点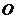 分别作
分别作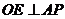 于点
于点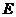 ,
,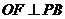 于点
于点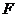 ,则
,则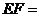 .
.
18.如图,小明在楼顶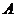 处测得对面大楼楼顶点
处测得对面大楼楼顶点 处的仰角为52°,楼底点
处的仰角为52°,楼底点 处的俯角为13°.若两座楼
处的俯角为13°.若两座楼 与
与 相距60米,则楼
相距60米,则楼 的高度约为 米.(结果保留三个有效数字)(
的高度约为 米.(结果保留三个有效数字)(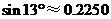 ,
,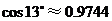 ,
,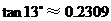 ,
,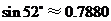 ,
,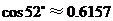 ,
, )
)

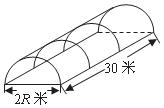
19.农村常需要搭建截面为半圆形的全封闭蔬菜塑料暖房如图所示,则需要塑料布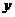 (m2)与半径
(m2)与半径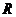 (m)的函数关系式是(不考虑塑料埋在土里的部分) .
(m)的函数关系式是(不考虑塑料埋在土里的部分) .
20.如图,已知双曲线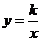 (
(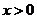 )经过矩形
)经过矩形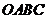 的边
的边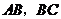 的中点
的中点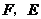 ,且四边形
,且四边形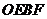 的面积为2,则
的面积为2,则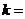 .
.
三、解答题(本大题共8道题,共计70分,解答时写出必要的文字说明、证明过程或演算步骤)
21.(本题满分6分)(1)一木杆按如图1所示的方式直立在地面上,请在图中画出它在阳光下的影子(用线段 表示);
表示);
(2)图2是两根标杆及它们在灯光下的影子.请在图中画出光源的位置(用点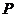 表示),并在图中画出人在此光源下的影子.(用线段
表示),并在图中画出人在此光源下的影子.(用线段 表示).
表示).
22.(本题满分7分)已知关于 的一元二次方程
的一元二次方程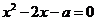 .
.
(1)如果此方程有两个不相等的实数根,求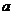 的取值范围;
的取值范围;
(2)如果此方程的两个实数根为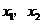 ,且满足
,且满足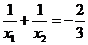 ,求
,求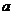 的值.
的值.
23.(本题满分7分)李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.
调查一:对小聪、小亮两位同学的毕业成绩进行调查,其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算,计算的方法按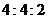 进行,毕业成绩达80分以上(含80分)为“优秀毕业生”,小聪、小亮的三项成绩如右表:(单位:分)
进行,毕业成绩达80分以上(含80分)为“优秀毕业生”,小聪、小亮的三项成绩如右表:(单位:分)
综合素质
考试成绩
体育测试
满分
100
100
100
小聪
72
98
60
小亮
90
75
95
调查二:对九年级(2)班50名同学某项跑步成绩进行调查,
并绘制了一个不完整的扇形统计图,如图14.
请你根据以上提供的信息,解答下列问题:
(1)小聪和小亮谁能达到“优秀毕业生”水平?哪位同学的毕业成绩更好些?
(2)升入高中后,请你对他俩今后的发展给每人提一条建议.
(3)扇形统计图中“优秀率”是多少?
(4)“不及格”在扇形统计图中所占的圆心角是多少度?

24.(本题满分9分)已知正比例函数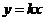 的图象与反比例函数
的图象与反比例函数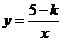 (
(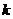 为常数,
为常数,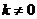 )的图象有一个交点的横坐标是2.
)的图象有一个交点的横坐标是2.
(1)求两个函数图象的交点坐标;
(2)若点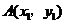 ,
,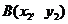 是反比例函数
是反比例函数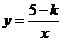 图象上的两点,且
图象上的两点,且 ,试比较
,试比较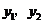 的大小.
的大小.
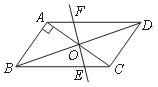
25.(本题满分9分)如图,平行四边形 中,
中,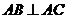 ,
, ,
,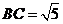 .对角线
.对角线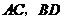 相交于点
相交于点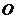 ,将直线
,将直线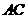 绕点
绕点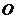 顺时针旋转,分别交
顺时针旋转,分别交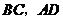 于点
于点 .
.
(1)证明:当旋转角为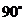 时,四边形
时,四边形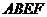 是平行四边形;
是平行四边形;
(2)试说明在旋转过程中,线段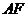 与
与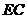 总保持相等;
总保持相等;
(3)在旋转过程中,四边形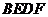 可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时
可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时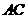 绕点
绕点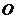 顺时针旋转的度数.
顺时针旋转的度数.
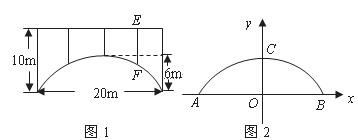
26.(本题满分10分)一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;
(2)求支柱 的长度;
的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.
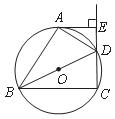
27.(本题满分10分)如图,四边形 内接于⊙
内接于⊙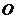 ,
,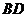 是⊙
是⊙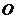 的直径,
的直径,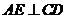 ,垂足为
,垂足为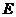 ,
,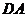 平分
平分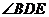 .
.
(1)求证: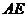 是⊙
是⊙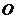 的切线;
的切线;
(2)若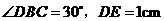 ,求
,求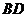 的长.
的长.
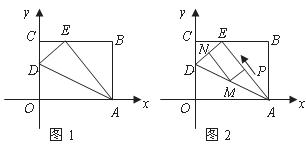
28.(本题满分12分)如图1,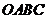 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片,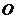 为原点,点
为原点,点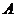 在
在 轴的正半轴上,点
轴的正半轴上,点 在
在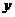 轴的正半轴上,
轴的正半轴上, ,
,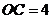 .
.
(1)在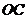 边上取一点
边上取一点 ,将纸片沿
,将纸片沿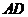 翻折,使点
翻折,使点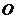 落在
落在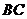 边上的点
边上的点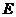 处,求
处,求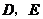 两点的坐标;
两点的坐标;
(2)如图2,若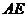 上有一动点
上有一动点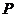 (不与
(不与 重合)自
重合)自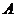 点沿
点沿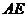 方向向
方向向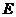 点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为
点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为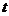 秒(
秒(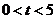 ),过
),过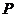 点作
点作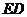 的平行线交
的平行线交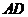 于点
于点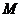 ,过点
,过点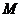 作
作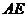 的平行线交
的平行线交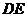 于点
于点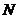 .求四边形
.求四边形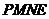 的面积
的面积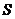 与时间
与时间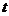 之间的函数关系式;当
之间的函数关系式;当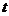 取何值时,
取何值时,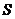 有最大值?最大值是多少?
有最大值?最大值是多少?
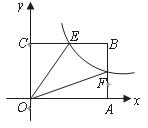
(3)在(2)的条件下,当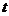 为何值时,以
为何值时,以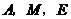 为顶点的三角形为等腰三角形,并求出相应的时刻点
为顶点的三角形为等腰三角形,并求出相应的时刻点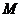 的坐标.
的坐标.