2008年临沂市初中学生学业考试与高中招生考试
数学试题
第Ⅰ卷(选择题 共42分)
一、选择题(本大题共14小题,每小题3分,共42分)在每小题所给的四个选项中,只有一项是符合题目要求的。
1.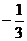 的倒数是
的倒数是
A.-3 B.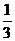 D.
D.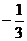
2.在今年四川汶川地震抗震救灾过程中,国内外社会各界纷纷伸出援助之手,截止到
A.3.99×108元 B.3.99×1010元
C.3.99×1011元 D.399×108元
3.下列各式计算正确的是
A.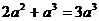 B.
B.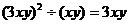
C. D.
D.
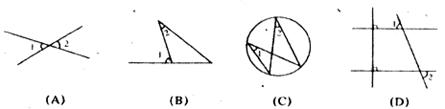
4.下列各图中,∠1大于∠2的是
5.计算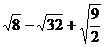 的结果是
的结果是
A.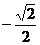 B.
B.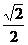 C.
C.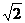 D.
D.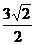
6.化简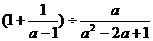 的结果是
的结果是
A.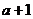 B.
B.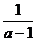 C.
C.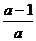 D.
D.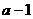
7.若不等式组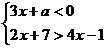 的解集为
的解集为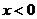 ,则
,则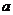 的取值范围为
的取值范围为
A.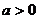 B.
B.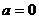 C.
C.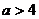 D.
D.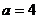
8.“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示)。小亮同学随机地在大正方形及其内部区域投针,若直角三角形的两条直角边的长分别是2和1,则针扎到小正方形(阴影)区域的概率是
A.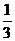 B.
B.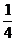 C.
C.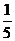 D.
D.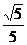
9.如图是一个包装盒的三视图,则这个包装盒的体积是
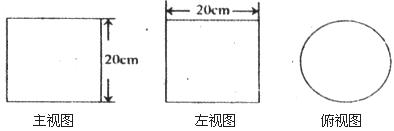
A.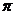 cm3 B.1500
cm3 B.1500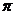 cm3
cm3
C.2000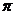 cm3 D.4000
cm3 D.4000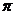 cm3
cm3
10.下列说法正确的是
A.随机事件发生的可能性是50%
B.一组数据2,3,3,6,8,5的众数与中位数都是3。
C.“打开电视机,正在播放关于奥运火炬传递的新闻”是必然事件。
D.若甲组数据的方差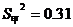 ,乙组数据的方差
,乙组数据的方差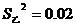 ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
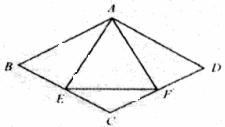
11.如图,菱形ABCD中,∠B=60º,AB=2,E,F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为
A.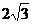 B.
B.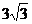 C.
C.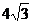 D.3
D.3
12.如图,直线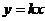
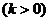 与双曲线
与双曲线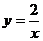 交于A、B两点,若A、B两点的坐标分别为
交于A、B两点,若A、B两点的坐标分别为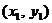 、
、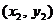 ,则的
,则的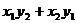 值为
值为
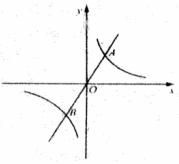
A.-8 B.4 C.-4 D.0
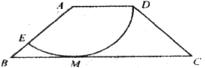
13.如图,等要梯形ABCD中,AD∥BC,以A为圆心,AD为半径的圆与BC切于点M,与AB交于点E,若AD=2,BC=6,则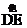 的长为
的长为
A.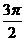 B.
B.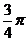 C.
C.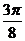 D.
D.
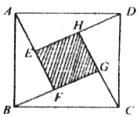
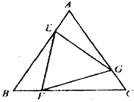
14.如图,已知正三角形ABC的边长为1,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为 ,AE的长为
,AE的长为 ,则
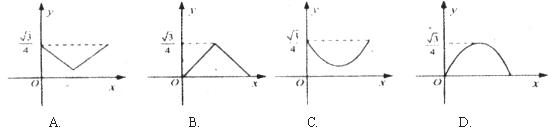
,则 关于
关于 的函数的图像大致是
的函数的图像大致是
第Ⅱ卷(非选择题 共78分)
二、填空题(本大题共5小题,每小题3分,共15分)把答案填在题中横线上。
15.分解因式: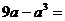 。
。
16.已知 、
、 满足方程组
满足方程组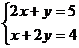 ,则
,则 的值为
。
的值为
。
17.某电动自行车厂三月份的产量为1000辆,由于市场需求量不断增大,五月份的产量提高到1210辆,则该厂四、五月份的月平均增长率为 。
18.如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,则CE的长为 。

19.如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,如此作下去。若OA=OB=1,则第 个等腰直角三角形的面积
个等腰直角三角形的面积 。
。

三、开动脑筋,你一定能做对!(本大题共3小题,共20分)
20.(本小题满分6分)
某油桃种植户今年喜获丰收,他从采摘的一批总质量为900千克的油桃中随机抽取了10个油桃,称得其质量(单位:克)分别为:106,99,100,113,111,97,104,112,98,110。
(1)估计这批油桃中每个油桃的平均质量;
(2)若质量不小于110克的油桃可定为优级,估计这批油桃中,优级油桃占油桃总数的百分之几?达到优级的油桃有多少千克?
21.(本小题满分7分)
如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= CD。
CD。
(1)求证:△ABF∽△CEB,
(2)若DEF的面积为2,求□ABCD得面积。

22.(本小题满分7分)
在某道路拓宽改造工程中,一工程队承担了24千米的任务,为了减少施工带来的影响,在确保工程质量的前提下,实际施工速度是原计划的1.2倍,结果提前20天完成任务,求原计划平均每天改造道路多少千米?
四、认真思考,你一定能成功!(本大题共2小题,共19分)
23.(本小题满分9分)
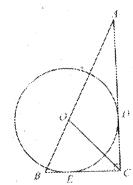
如图,Rt△ABC中,∠ACB=90º,AC=4,BC=2,以AB上的一点O为圆心的圆分别与AC、BC相切与点D、E。
(1)求⊙O的半径;
(2)求sin∠BOC得值。
24.(本小题满分10分)
某商场欲购进A、B两种品牌的饮料共500箱,此两种饮料每箱的进价和售价如下表所示。设购进A种饮料 箱,且所购进的两种饮料能全部卖出,获得的总利润为
箱,且所购进的两种饮料能全部卖出,获得的总利润为 元。
元。
品牌
A
B
进价(元/箱)
55
35
售价(元/箱)
63
40
(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)如果购进两种饮料的总费用不超过20000元,那么该商场如何进货才能获利最多?并求出最大利润。(注:利润=售价-进价)
五、相信自己,加油呀!(本大题共2小题,共24分)
25.(本小题满分11分)
已知∠MAN,AC平分∠MAN。

(1)在图1中,若∠MAN=120º,∠ABC=∠ADC=90º,求证AB+AD=AC;
(2)在图2中,若∠MAN=120º,∠ABC+∠ADC=180º,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;
(3)在图3中
①若∠MAN=60º,∠ABC+∠ADC=180º,则AB+AD= AC;
②若∠MAN=α(00<α<180º),∠ABC+∠ADC=180º,则AB+AD= AC(用含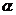 的三角函数表示),并给出证明。
的三角函数表示),并给出证明。
26.(本小题满分3分)
如图,已知抛物线与 轴交于A(-1,0)、B(3,0)两点,与
轴交于A(-1,0)、B(3,0)两点,与 轴交于点C(0,3)。
轴交于点C(0,3)。
(1)求抛物线的解析式;
(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形,若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)若点M是抛物线上一点,以B、C,D、M为顶点的四边形是直角梯形,试求出点M的坐标。