摘要:②若∠MAN=α(00<α<180º),∠ABC+∠ADC=180º.则AB+AD= AC(用含的三角函数表示).并给出证明.
网址:http://m.1010jiajiao.com/timu_id_725739[举报]
已知∠MAN,AC平分∠MAN。
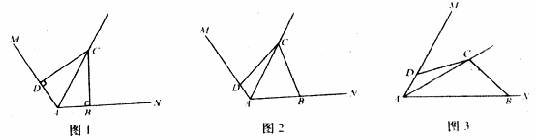
(1)在图1中,若∠MAN=120º,∠ABC=∠ADC=90º,求证AB+AD=AC;
(2)在图2中,若∠MAN=120º,∠ABC+∠ADC=180º,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;
(3)在图3中
①若∠MAN=60º,∠ABC+∠ADC=180º,则AB+AD= AC;
②若∠MAN=α(00<α<180º),∠ABC+∠ADC=180º,则AB+AD= AC(用含![]() 的三角函数表示),并给出证明。
的三角函数表示),并给出证明。
已知∠MAN,AC平分∠MAN。
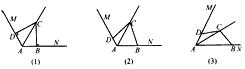
(1)在图(1)中,若∠MAN=120°,∠ABC=∠ADC=90°,则AB+AD____AC;(填写“>”“<”或“=”)
(2)在图(2)中,若∠MAN=120°,∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)在图(3)中:
①若∠MAN=60°,∠ABC+∠ADC=180°,判断AB+AD与AC的数量关系,并说明理由;
②若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,则AB+AD=____AC。(用含α的三角函数表示,直接写出结果,不必证明)
查看习题详情和答案>>
(2)在图(2)中,若∠MAN=120°,∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)在图(3)中:
①若∠MAN=60°,∠ABC+∠ADC=180°,判断AB+AD与AC的数量关系,并说明理由;
②若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,则AB+AD=____AC。(用含α的三角函数表示,直接写出结果,不必证明)
(本小题满分14分)
如图①,已知四边形ABCD是正方形,点E是AB的中点,点F在边CB的延长线上,且BE=BF,连接EF.

1.(1)若取AE的中点P,求证:BP= CF;
CF;
2.(2)在图①中,若将 绕点B顺时针方向旋转
绕点B顺时针方向旋转 (00<
(00< <3600),如图②,是否存在某位置,使得
<3600),如图②,是否存在某位置,使得 ?,若存在,求出所有可能的旋转角
?,若存在,求出所有可能的旋转角 的大小;若不存在,请说明理由;
的大小;若不存在,请说明理由;
3.(3)在图①中,若将△BEF绕点B顺时针旋转 (00<
(00< <900),如图③,取AE的中点P,连接BP、CF,求证:BP=
<900),如图③,取AE的中点P,连接BP、CF,求证:BP= CF且BP⊥CF.
CF且BP⊥CF.
查看习题详情和答案>>

 (00<
(00<
 CF;
CF; 绕点B顺时针方向旋转
绕点B顺时针方向旋转 (00<
(00< ?,若存在,求出所有可能的旋转角
?,若存在,求出所有可能的旋转角