安庆市皖河中学学业水平测试数学复习卷
必修(三) 2008-6-3
班级: 姓名: 学号: 成绩:
考生注意:
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分为150分.考试时间120分钟.
第I卷 (选择题 共60分)
一、选择题 本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是最符合题目要求的,请把正确的答案填在题后的括号内。
A. ①② B. ②③ C. ③④ D. ②④
(3)用秦九韶算法计算多项式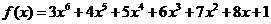 ,当
,当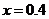 时的值时,需要做乘法和加法的次数分别是……………………………………………………()
时的值时,需要做乘法和加法的次数分别是……………………………………………………()
A.6,6 B.5,6 C.5,5 D.6,5
(4)下列各数中最小的数是……………………………………………………………………()
A.111111(2) B.210(6) C.100(4) D.71(8)
(5)某中学组织春游,为了确定春游地点,打算从学校学号为0034~2037的所有学生中,采用系统抽样抽取50名进行调查,学号为2003的同学被抽到的可能性为…………………()
A.1/2003 B.1/2004 C.50/2003 D.50/2004
(6)10名工人某天生产同一件零件,生产的件数是15,17,14,10,15,17,17,16,14,14。设其平均数为a,中位数为b,众数为c,则有…………………………………………()
A.a>b>c B.b>c>a C.c>a>b D.c>b>a
(7)一组数据的方差为s2,将这组数据中每个数据都扩大到原来的2倍,所得到的新数据的方差是…………………………………………………………………………………………()
A. s2 B. 2s2 C. 3s2 D. 4s2
X
0
1
2
3
y
1
3
5
7
(8)已知之间的一组数据如右表所示,则y与x的线性回归方程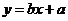 必过…………………………………………………………()
必过…………………………………………………………()
 A.(2, 2)点 B.(1.5, 0)点
A.(2, 2)点 B.(1.5, 0)点
C.(1, 2)点 D.(1.5, 4)点
(9)右图所示的茎叶图表示某城市一台自动售货机的销售额情况,那么这组数据的级差是………………………………………………………………………()
A.9 B.39 C.41 D.59
(10)“将一根木棍折成三段,拼成一个三角形”,这个事件是………………………………()
A.随机事件 B.必然事件 C.不可能事件 D.以上都不对
(11)同时掷两个骰子,那么下列两个事件互斥而不对立的是………………………………()
 A. “点数之和为奇数”与“点数之和为偶数” B.“点数之和为偶数”与“点数之和为质数”
A. “点数之和为奇数”与“点数之和为偶数” B.“点数之和为偶数”与“点数之和为质数”
C.“点数之和为3的倍数”与“点数之和为4的倍数”
D.“点数之和为奇数”与“点数之和为4的倍数”
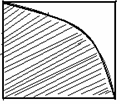
(12)在正方形内有一扇形(见阴影部分),点随意等可能落在正方形
内,这点落在扇形外正方形内的概率为…………………………………()
A. B.
B.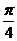 C.
C.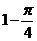 D.
D.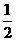
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
INPUT “M=”; M
N=M
M=2*6
P=(M*N)/2
Q=N*P
PRINT M, N, P, Q
END
第Ⅱ卷(非选择题 共90分)
(13)在右边程序中,如果输入的是3,则运行结果是 。
(14)下列程序中:INPUT a
IF a<0 THEN
二、填空题 本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
b = 0.5 * a
ELSE
b = a^2 + 3*a + 1
END IF
PRINT b
END
若a = 4,则b = ;若a= -- 4,则b = 。
(15)从甲、乙、丙、丁四个候选人中选出3名代表参加团代会,甲一定入选的概率是 。
(16)在下列说法中:
①既然抛掷硬币出现正面的概率是0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上; ②如果某种彩票的中奖概率为1%,那么买1000张这种彩票一定能中奖; ③在乒乓球、排球等比赛中,裁判通过让运动员猜上抛均匀塑料圆板着地是正面还是反面来决定哪一方先发球,这样做公平; ④一个骰子掷一次得到6的概率是1/6,这说明一个骰子掷6次会出现一次6。
其中不正确的说法是 。
(17)(本小题满分10分)将下列问题的算法用UNTIL语句表示,并画出程序框图。(写在下面的框中)
三、解答题 本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.

 i=1
i=1
S=0
WHILE i≤10
S=S+i
i=i+1
WEND
PRINT S
END
(18)(本小题满分12分)在游乐场,有一种游戏是向一个画满均匀方格的大桌面上投硬币。若硬币刚巧落在任何一个方格内(不与方格线重合),便可获奖。如果硬币的直径为2厘米,而方格的边厂为5厘米,则随机投掷一个硬币,获奖的概率有多大?
(19)(本小题满分12分)从高三学生中抽取50名同学参加知识竞赛,成绩分组及各组的频数如下(单位:分):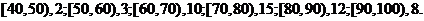
(Ⅰ)列出样本频率分布表(含累积频率); (Ⅱ)画出频率分布直方图;
(Ⅲ)估计成绩在[60,90)内学生的频率; (Ⅳ)估计成绩在85分以下的学生的频率。
(20)(本小题满分12分)三人制篮球队由一个后卫、一个中锋和一个前锋组成。现从不同的三个三人制篮球队各选一人。试求:
(Ⅰ)正好组成一个完整球队的概率是多少?
(Ⅱ)被选的三人都打同一位置的概率是多少?
(21)(本小题满分14分)若有三个不同大小的数字,你能设计一个算法,找出其中的最大值吗?给出解决问题的一种算法,并画出流程图。
(22)(本小题满分14分)要分析初中升学的数学成绩对高一年级数学学习有什么影响,在高一年级学生中随机抽选10名学生,分析他们入学的数学成绩和高一年级期末数学考试成绩:
学生编号
1
2
3
4
5
6
7
8
9
10
入学成绩(x)
63
67
45
88
81
71
52
99
58
76
高一期末成绩(y)
65
78
52
82
92
89
73
98
56
75
(Ⅰ)画出散点图;
(Ⅱ)求出线性回归方程;
(Ⅲ)若某学生入学成绩为80分,试估计他在高一年级期末数学考试成绩。