2008年贵阳市中考模拟试卷九
数学
一、选择题(以下每小题都有A、B、C、D四个选项。其中只有一个选项正确,请把正确选项的字母选入该题的括号内。每小题4分,共20分)
1.一3的平方是( ).
A.3 B.9 C.一9 D.一3
2.小明五次跳远的成绩(单位:米)是:3.6,3.8,4.2,4.0,3.9,这组数据的中位数是( ).
A.3.9米 B.3.8米 C.4.2米 D.4.0米
3.如下图有一边长为6cm的等边三角形ABC木块,点P是CA的延长线上的点,AP为15cm,其中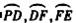 的圆心依次为A,B,C,则曲线PDFE的长是( )cm.
的圆心依次为A,B,C,则曲线PDFE的长是( )cm.

A.18 B.15
B.15 C.20
C.20 D.21
D.21
4.平面直角坐标系中有六个点A(1,5),B( ),C(
),C(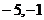 ),D(
),D(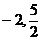 ),E(3,
),E(3, ),F(
),F(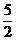 ,2),其中有五个点在同一反比例函数图像上,不在这个反比例函数图像上的点是( ).
,2),其中有五个点在同一反比例函数图像上,不在这个反比例函数图像上的点是( ).
A.点C B.点D C.点E D.点F
5.如下图,将(1)所示长为20cm,宽为2cm的长方形白纸条,折成(2)所示的图形并在其 一面着色,则着色部分的面积为( ).
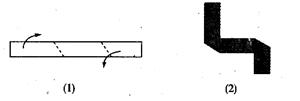
A.34cm2 B.36cm2 C.38cm2 D.40cm2
二、填空题(每小题3分,共30分)
6.分解因式: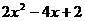 =
.
=
.
7.5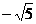 的整数部分是
.
的整数部分是
.
8.股市有风险,投资须谨慎.截至2007年5月底,我国股市开户总数约95000000,正向1亿挺进,95000000用科学记数法表示为 .
9.在一次抽奖活动中,中奖概率是0.12,则不中奖的概率是 .
10.用计算器计算:3sin38°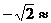 .(结果保留3个有效数字)
.(结果保留3个有效数字)
11.如下图,已知∠1=100°,∠2=140°,那么∠3= 度.
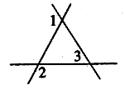
12.两个小组进行定点投篮对抗赛.每组6名组员,每人投10次,两组组员进球数统计结果如下:
组别
6名组员的进球数
平均数
甲组
8
5
3
1
1
0
3
乙组
5
4
3
3
2
1
3
则组员投篮水平较整齐的小组是 .
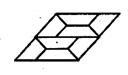
13.如下图,是用形状、大小完全相同的等腰梯形密铺成的图案,则这个图案中的等腰梯形的底角(指钝角)是 .
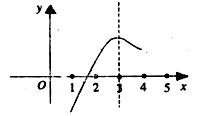
14.已知二次函数 的部分图像,如下图所示,由图像可知关于
的部分图像,如下图所示,由图像可知关于 的一元二次方程
的一元二次方程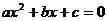 的两个根分别是
的两个根分别是 ,
,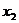 =
.
=
.
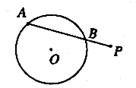
15.如下图,某机械传动装置在静止状态时,连杆PA与点A运动所形成的圆O交于B点,现测得PB=4cm,AB=5cm,圆D的半径R=4.5cm,此时P点到圆心O的距离是 cm.
三、解答题
16.(本题7分)
给定下面一列分式: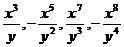 (其中
(其中 ≠0)
≠0)
(1)把任意一个分式除以前面一个分式,你发现了什么规律?(3分)
(2)根据你发现的规律,试写出给定的那列分式中的第7个分式.(4分)
17.(本题10分)
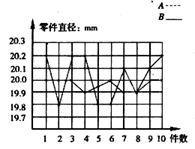
某学校为选派一名学生参加全市劳动技能竞赛,准备从A、B两位同学中选定一名,A,B两位同学在学校实习基地进行现场加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据如下图和下表所示(单位:mm).
根据测试得到的有关数据,请解答下面的问题:
(1)考虑平均数与完全符合要求的个数,你认为谁的成绩要好些?(2分)
(2)计算出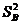 的值,考虑平均数与方差,你又认为谁的成绩要好些?(5分)
的值,考虑平均数与方差,你又认为谁的成绩要好些?(5分)
(3)根据折线图的走势,你认为派谁去参赛较合适?说明你的理由.(3分)
平均数
方差
完全符合
要求个数
A
20
0.026
2
B
20
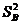
5
18.(本题7分)
下图所示某闭合电路中,电源的电压为定值,电流I(A)与电阻R(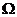 )成反比例。
)成反比例。
(1)请观察图像,并根据图上的数据求出I与R的关系式;(4分)
(2)根据图像写出当电阻R>3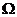 时,电流I的取值范围.(3分)
时,电流I的取值范围.(3分)
19.(本题10分)
如下图,一枚运载火箭从地面O处发射,当火箭到达A点时,从地面C处的雷达站测得AC的距离是6km,仰角是43°.1s后,火箭到达B点,此时测得BC的距离是6.13km,仰角为45.54°.解答下列问题:
(1)火箭到达B点时距离发射点多远?(精确到0.01km);(4分)
(2)火箭从A点到B点的平均速度是多少? (精确到0.1km/s)(6分)

20.(本题10分)
如下图,在△ABC中AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,
(1)求证:△BDE≌△CDF;(5分)
(2)当∠A=90°时,四边形AEDF是什么四边形?请证明你的结论.(5分)

21.(本题10分)
一等奖
二等奖
三等奖
一盒福娃和1枚徽章
一盒福娃
1枚徽章
用于购买奖品的总费用不少于1000元但不超过1100元,小明购买“福娃”和徽章前,了解到如下信息:
学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
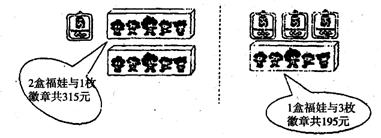
(1)求一盒“福娃”和一枚徽章各多少元?(6分)
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?(4分)
22.(本题12分)
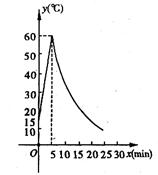
制作一种产品,需先将材料加热达到60℃后,再进行操作,设该材料温度为y(℃),从加热开始计算的时间为 (min).据了解,设该材料加热时,温度y与
(min).据了解,设该材料加热时,温度y与 时间成一次函数关系;停止加热进行操作时,温度y与时间
时间成一次函数关系;停止加热进行操作时,温度y与时间 成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和停止加热进行操作时,y与 函数关系式;(6分)
函数关系式;(6分)
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?(6分)
23.(本题10分)
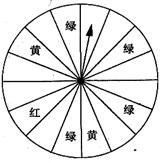
在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,转盘被平均分成16份,并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券10元.
(1)求每转动一次转盘所获购物券金额的平均数;(6分)
(2)如果你在该商场消费125元,你会选择转转盘还是直接获得购物券?说明理由。(4分)
24.(本题12分)
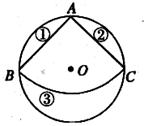
如图,从一个直径是2的圆形铁皮中剪下一个圆心为90°的扇形。
(1)求这个扇形的面积(结果保留 );(4分)
);(4分)
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.(4分)
(3)当圆O的半径R(R>0)为任意值时,(2)中的结论是否仍然成立?请说明理由。(4分)
25.(本题12分)
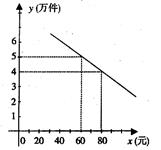
某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量y(万件)与销售单价 (元)之间存在着如图所示的一次函数关系.
(元)之间存在着如图所示的一次函数关系.
(1)求y关于 的函数关系式;(5分)
的函数关系式;(5分)
(2)试写出该公司销售该种产品的年获利z(万元)关于销售单价 (元)的函数关系式,当销售单价
(元)的函数关系式,当销售单价 为何值时,年获利最大?并求这个最大值.(7分)
为何值时,年获利最大?并求这个最大值.(7分)