摘要:20. 如下图.在△ABC中AB=AC.D是BC的中点.DE⊥AB.DF⊥AC.垂足分别为E.F. (1)求证:△BDE≌△CDF, (2)当∠A=90°时.四边形AEDF是什么四边形?请证明你的结论.
网址:http://m.1010jiajiao.com/timu_id_695223[举报]
(本题满分10分)如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.

1.(1)求证:四边形AFBD是平行四边形;
2.(2)将下列命题填写完整,并使命题成立(图中不再添加其它的点和线):
① 当△ABC满足条件AB=AC时,四边形AFBD是 形;
② 当△ABC满足条件 时,四边形AFBD是正方形.
查看习题详情和答案>>
(本题满分10分)如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.

1.(1)求证:四边形AFBD是平行四边形;
2.(2)将下列命题填写完整,并使命题成立(图中不再添加其它的点和线):
① 当△ABC满足条件AB=AC时,四边形AFBD是 形;
② 当△ABC满足条件 时,四边形AFBD是正方形.[来源:Zxxk.Com]
时,四边形AFBD是正方形.[来源:Zxxk.Com]
查看习题详情和答案>>
(本小题满分10分)
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
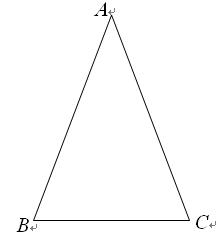
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=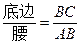 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad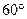 的值为( )
的值为( )
(2)对于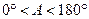 ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .
(3)已知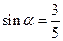 ,其中
,其中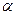 为锐角,试求sad
为锐角,试求sad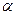 的值.
查看习题详情和答案>>
的值.
查看习题详情和答案>>
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
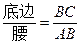 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题:

(1)sad
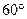 的值为( )
的值为( )A. | B.1 | C.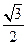 | D.2 |
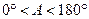 ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .(3)已知
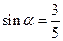 ,其中
,其中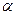 为锐角,试求sad
为锐角,试求sad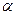 的值.
查看习题详情和答案>>
的值.
查看习题详情和答案>>
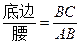 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.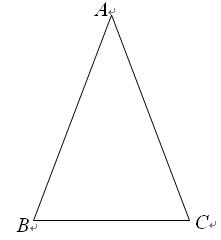
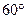 的值为( )
的值为( )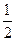
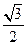
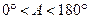 ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .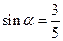 ,其中
,其中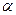 为锐角,试求sad
为锐角,试求sad