1．在-2,л,3.14,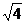,cos45⁰,(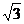)⁰中，有理数的个数是（   ）

A. 2   B.3    C. 4   D.5

2．用一批形状完全相同的正多边形地板砖铺地面，要求顶点聚在一起，砖与砖间不留空隙，现有①正三角形、②正方形、③正五边形、④正六边形、⑤正八边形五种类型的地板砖，则符合要求的有（   ）

A. ①②③   B. ②③④⑤    C. ①③④⑤   D. ①②④

3．某服装商同时卖出两套服装，每套均为168元，以成本计算，其中一套盈利20%，另一套亏本20%，这次出售商家（    ）

A. 不赚不赔   B.赔14元    C. 赚14元   D.赚37.2元

4．第五次人口普查结果显示，我国总人口已达到1300000000人，把这个数保留三个有效数字，并用科学记数法表示应为（    ）

A. 1.30´10⁹   B. 1.30´10⁸     C.0. 13´10¹⁰    D. 0.130´10⁹

5．若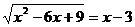，则x的取值范围是（ ）

A.x＞3 　　 B.x≥3   C.x＜3　　 D.x≤3   

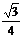6．用半圆纸片围成圆锥，则圆锥的高与底面半径的比是（  ）  

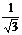
 A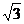． 　　B．    　C．   　　  D．

７．为了调查初二学生完成家庭作业所需的时间，在某校抽查了8名学生他们完成作业所需时间分别为：75、70、90、70、70、58、80、55（单位：分钟）则这组数据的众数、中位数和平均数依次是（　　）

A．70、70、71　　　　B．70、71、70    C．71、70、70　　D．70、70、70

８.甲乙两人练习跑步，甲先让乙跑１０米，则甲５秒钟追上乙，若甲让乙先跑２秒，甲跑４秒就追上乙，甲乙两人每秒分别跑（　　）　　

A．４米、６米　　　B．２米、４米     C．６米、４米　　　D．４米、２米

第II卷（非选择题  共96分）

１．小明身高１.5米，他站在教学楼前３０米处，以３０⁰仰角刚刚看到楼顶，此楼高为　　　　　米。（保留３个有效数字）

２．若将４根木条钉成的矩形木框变形为平行四边形形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的值是　　　　。

３．对角线互相垂直一部分的四边形是         。

4、DABC中，D为AC上一点，要使DABC~DBDC，则必须具备的条件是             。（只填写一个即可）

5、小明家4月份前6天用米量如下表(单位：千克)

日期

1号

2号

3号

4号

5号

6号

用米量

0.9

0.8

0.6

0.9

0.8

1.0

估计小明家4月份（30天）用米总量为         千克。

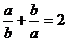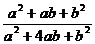6、若a、b 满足  ，则的值是         。

7、多项式9x²+1加上一个单项式，使它成为一个整式的完全平方，则这个单项式可以是                    。（答案有多个，只填写符合条件的一个即可）

8、有一边长为2cm的正六边形，若要剪一圆形纸片完全盖住它，则圆纸片的最小半径是            。

1．（8分）化简并求值

已知实数a满足a²+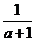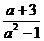2a-8=0，求 - ?的值。

2、（10分）某公司到果园基地购买某种优质水果以慰问医务工作者，果园基地对购买量在3000千克以上（含3000千克）的有两种销售方案．甲方案：每千克9元，由基地送货上门；乙方案，每千克8元，由顾客自己租车运回，已知该公司租车从基地到公司的运输费为5000元．

（１）分别写出该公司两种购买方案的付款ｙ（元）与所购买的水果量ｘ（千克）之间的函数关系式，并写出自变量ｘ的取值范围；

（２）当购买量在什么范围时，选择哪种购买方案付款最少？并说明理由。

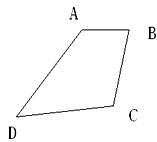
3．（8分）某公园有一个呈四边形的小湖（如图）在它的四个角A、B、C、D上都有一棵古树，现公园管理处想扩大湖面，使湖面扩大一倍，形状为平行四边形，且不破坏古树，请问公园的这一设想能够实现吗？若能，请你画出设计图形，若不能请说明理由（画图并保留痕迹，不写画法）。

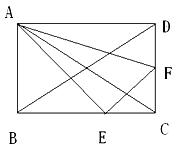
4．（10分）如图，矩形ABCD中，BD=20，AD›AB，∠ABD=α，且sinaα是方程25x²-35x+12=0的一个实数根，EC+CF=8，令BE=x，ㄓAEF的面积为y。

（1）求y与x的函数关系式。

（2）当E、F两点在什么位置时， y有最小值，并求出这个最小值。

5．（10分）某居民小区有一朝向正南方的居民楼，该居民楼的一楼为高6米的超市，超市以上是居民住房，在该楼正南方15米处建一高20米的新楼，当冬季太阳光与水平线夹角为32⁰时。

（1）问超市以上居民住房的采光是否受到影响？（5分）

（2）若要使超市采光不受影响，两楼应相距多少米？（5分）

（结果保留整数，参考数据 sina32⁰=,cos32⁰=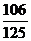,tg32⁰=）

6．(12分)已知， 如图，⊙O的直径为AB,PC切⊙O于C,AD⊥PC于D,CM⊥AP于M.

（1）求证：CB平分∠MCP.

（2）若PO=5,PC=a, ⊙O的半径为r，且a、r为方程x²-(2m+1)x+4m=0的两个根，求m.

7.(14分)某商业公司为指导某种应季商品的生产和销售，对三月份至七月份该商品的售价和成本进行了调研，结果如下：每件商品的售价M（元）与时间t（月）的关系可用一条线段上的点来表示（如图1），每件商品的成本Q（元）与时间t（月）的关系可用一条抛物线的一部分上的点来表示（如图2）。

（说明：图1、图2中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本。）
请你根据图象提供的信息回答：
   （1）每件商品在3月份出售时的利润（利润＝售价－成本）是多少元？

（2）求图2中表示的每件商品的成本Q（元）与时间t（月）之间的函数关系式（不要求写自变量的取值范围）；

（3）你能求出三月份至七月份每件商品的利润W（元）与时间t（月）之间的函数关系式吗？（请写出计算过程，不要求写自变量的取值范围）若该公司共有此种商品30000件，准备在一个月内全部售完，请你计算一下至少可获利多少元？