2007-2008学年度江苏省太仓市初三第一学期期末考试
数学试卷
本试卷总分共130分,考试时间120分钟
一、选择题:把下列各题正确答案前面的英文字母填入答题卷相应位置的表格内.(每小题3分,共18分)
1.如图,CD是Rt△ABC斜边上的高,AC=4,BC=3.则cos∠BCD的值是
A.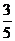 B.
B.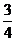 C.
C.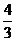 D.
D.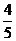
2.已知关于 的一元二次方程
的一元二次方程 ,若用配方法解该方程,则配方后的方程是
,若用配方法解该方程,则配方后的方程是
A. B.
B.
C. D.
D.
3.与抛物线 顶点相同,形状也相同,而开口方向相反的抛物线对应的函数是
顶点相同,形状也相同,而开口方向相反的抛物线对应的函数是
A. B.
B.
C. D.
D.
4.如图,A、B、C是⊙O的三点,∠AOC=40°,则∠ABC的大小是
A.10° B.20° C.40° D.80°
5.一只小虫从A点出发,在坡度为1:7的斜坡上爬到点B,当AB=
A. B.
B.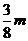 C.
C. D.以上均不对
D.以上均不对
6.如图,一扇形纸扇完全打开后,外侧两个木条,AB、AC的夹角为120°,AB长为

A.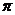 cm2 B.500
cm2 B.500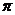 cm2 C.
cm2 C.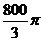 cm2 D.
cm2 D.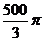 cm2
cm2
二、填空题:(每小题3分,共36分)
7.抛物线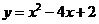 的顶点坐标为
.
的顶点坐标为
.
8.若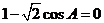 ,则锐角A= .
,则锐角A= .
9.在Rt△ABC中,∠C=90°,3a=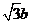 ,则sinA=
.
,则sinA=
.
10.若关于 的方程
的方程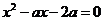 的一个根是3,则它的另一根是
.
的一个根是3,则它的另一根是
.
11.若代数式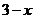 与
与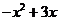 的值互为相反数,则
的值互为相反数,则 的值是 .
的值是 .
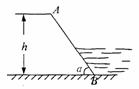
12.如图,是一水库大坝横断面的一部分,坝高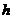 =6m,近水斜坡AB=10m,斜坡的坡角为
=6m,近水斜坡AB=10m,斜坡的坡角为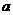 ,则tan
,则tan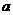 的值是
.
的值是
.
13.将抛物线 向右平移3个单位后,所得抛物线的顶点坐标是
.
向右平移3个单位后,所得抛物线的顶点坐标是
.
14.正方形ABCD的边长是2cm,以直线AB为轴旋转一周,所得到的圆柱的侧面积为 
15.已知两圆的半径分别为3和4,圆心的坐标分别是点(0,3)、(4,0),那么这两圆的位置关系是 .
16.要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要 cm
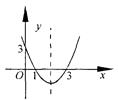
17.抛物线的图象如图,则它关于y轴对称的抛物线的表达式是 .
18.若过⊙O内一点P的最长的弦为l0cm, 最短弦长为8cm,则OP的长为 .
三、解答题:(共11小题,76分,解答时应写出文字说明,证明过程和演算步骤)
19.计算.(每小题3分,共6分)
(1)
(2)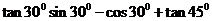
20.(本题6分)如图,在△ABC中,AD是BC边上的高,tanB=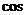 ∠DAC,
∠DAC,

(1)AC和 BD相等吗?为什么?
(2)若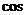 C=
C=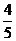 ,BC=12,求AC的长.
,BC=12,求AC的长.
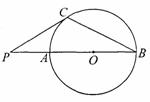
21.(本题6分)如图,点P在⊙O的直径BA 的延长线上,AB=2PA,PC切⊙O于点C,连结BC,
(1)求∠P的正弦值:
(2)若⊙O的半径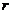 =2cm,求BC的长度.
=2cm,求BC的长度.
22.(本题6分)已知抛物线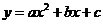 与抛物线
与抛物线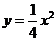 形状相同,顶点坐标为
形状相同,顶点坐标为
(-2,4),求a,b,c的值.
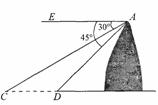
23.(本题6分)如图,河旁有一座小山,从山顶A处测得对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米,现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长.
24.(本题8分)△ABC中,∠A,∠B,∠C的对边分别为a,b,c,已知关于 的方程
的方程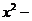
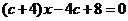
(1)若a,b是方程的两根,求证△ABC为直角三角形;
(2)若在(1)的条件下,且25asinA=9c,求此直角一角形三边的长.
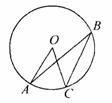
25.(本题8分)如图,已知点A、B、C、D均在已知圆上,AD∥BC,CA平分∠BCD,∠ADC=l20°,四边形ABCD的周长为10,
(1)求此圆的中径:
(2)求圆中阴影部分的面积.

26.(本题10分)矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0)、C(0,3),直线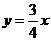 与BC边相交于点D,
与BC边相交于点D,
(1)求点D的坐标:
(2)若抛物线 经过D、A两点,试确定此抛物线的表达式:
经过D、A两点,试确定此抛物线的表达式:
(3)P为 轴上方(2)题中的抛物线上一点,求△POA面积的最大值.
轴上方(2)题中的抛物线上一点,求△POA面积的最大值.

27.(本题10分)如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连结DB、DE、OC.
(1)从图中找出一对相似三角形(不添加任何字母及辅助线),并证明你的结沦;
(2)若AD=2,AE=l,求CD的长.

28.(本题10分)已知:射线OF交⊙O于点B,半径OA⊥OB,P是射线OF上的一个动点(不与O、B垂直)直线AP交⊙O于D,过D作⊙O的切线交射线OF于E.
(1)图1是点P在侧内移动时符合已知条件的图形,请你在图2中画出点P在圆外移动时符合己知条件的图形;

(2)观察图形,点P在移动过程中,△DPE的边、角或形状存在某些规律,请你通过观察、测量、比较,写出一条与△DPE的边,角或形状有关的规律;
(3)在点P移动过程中,设∠DEP的度数为x,∠OAP的度数为y,求y与x的函数关系式,并写出自变量 的取值范围.
的取值范围.