2006-2007学年度北京市宣武区第二学期第二次质量检测
初三数学试题
第Ⅰ卷(选择题共32分)
一、选择题(共8个小题。每小题4分,共32分)下列各题均有四个选项,其中只有一个是符合题目要求的。
1.9的算术平方根是( )
A.3 B.-
2.半径为3和5的两圆相外切,则其圆心距为( )
A.l6 B.
3.某鞋店试销某种品牌的运动鞋,营业员按鞋型号记录了1个月的销售情况,她最关心的是鞋型号的( )
A.平均数 B.中位数 C.众数 D.加权平均数
4.如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,DB=2,则 的值为( )
的值为( )

A. B.
B. C.
C. D.2
D.2
5.设 ,则实数
,则实数 在数轴上对应的点的大致位置是( )
在数轴上对应的点的大致位置是( )

6.直线 与双曲线
与双曲线 的一个分支(
的一个分支( )相交,则该分支的图象大致是下面的图( )
)相交,则该分支的图象大致是下面的图( )

7.下列左边的主视图和俯视图对应右边的哪个物体( )

8.根据下列表格的对应值:

3.23
3.24
3.25
3.26
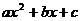
-0.06
-0.02
0.03
0.09
判断方程 (
( ,
, ,
, ,
, 为常数)一个解
为常数)一个解 的范围是( )
的范围是( )
A. B.
B.
C. D.
D.
第Ⅱ卷(非选择题 共88分)
二、填空题(共4个小题,每小题4分,共16分)
9.函数 的自变量
的自变量 的取值范围是
。
的取值范围是
。
10.某中学对200名学生进行了关于“造成学生睡眠少的主要原因”的抽样调查,将调查结果制成扇形统计图,由图中的信息可知认为“造成学生睡眠少的主要原因是作业太多”的人数有 名。

11.如图,在方格纸中, 、
、 、
、 这三个角的大小关系是
。
这三个角的大小关系是
。
12.在实数的原有运算法则中,我们补充定义新运算“*”如下:
当 时,
时, ;当
;当 时,
时,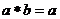 ,
,
则当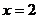 时,
时,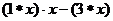 的值为 。(“?”和“-”仍为实数运算中的乘号和减号)
的值为 。(“?”和“-”仍为实数运算中的乘号和减号)
13.分解因式: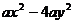
14.解方程: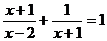 。
。
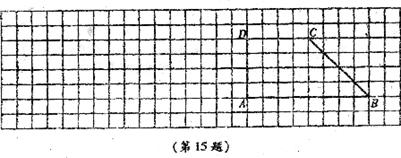
15.在下面的网格图中,先画出梯形ABCD以点B为位似中心,缩小到 后得到的梯形A1BC1D1;再画出梯形A1BC1D1向左平移15格后得到的梯形A2B
后得到的梯形A1BC1D1;再画出梯形A1BC1D1向左平移15格后得到的梯形A2B
四、解答题(共4个小题.每小题5分,共20分)
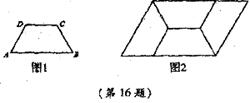
16.如图l,四边形ABCD是等腰梯形,AB∥DC。由4个这样的等腰梯形可以拼出图2所示的平行四边形。
(1)求四边形ABCD四个内角的度数;
(2)求证:梯形ABCD的上底等于下底的一半。
17.三人相互传球,由甲开始发球,并作为第一次传球,请用列表或画树状图的方法求经过3次传球后,球仍回到甲手中的概率是多少?
18.五一黄金周期间。李娟同学和父母自驾车外出旅游。出发时,里程表显示0千米,余油量表显示 升,行驶过程中每千米耗油
升,行驶过程中每千米耗油 升。途中李娟同学两次观察里程表和余油量表,当里程表显示30千米时,余油量表显示
升。途中李娟同学两次观察里程表和余油量表,当里程表显示30千米时,余油量表显示 千米,油箱中的余油量为
千米,油箱中的余油量为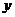 升,求出
升,求出 、
、 值,并写出
值,并写出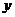 关于
关于 的函数关系式。
的函数关系式。
19.如图,边长为1的正方形OABC的顶点A在 轴的正半轴上,将正方形OABC绕点O顺时针旋转30°,使点A落在抛物线
轴的正半轴上,将正方形OABC绕点O顺时针旋转30°,使点A落在抛物线 上,求抛物线
上,求抛物线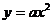 的函数关系式。
的函数关系式。

五、解答题(共3个小题,每小题6分,共l8分)
20.已知一元二次方程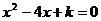 有两个不相等实数根。
有两个不相等实数根。
(1)求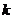 的取值范围;
的取值范围;
(2)如果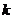 是符合条件的最大整数,且―元二次方程
是符合条件的最大整数,且―元二次方程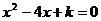 与
与 有一个相同的根,求此时
有一个相同的根,求此时 的值。
的值。
21.如图,在Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AD=BC,AC、BD相交于点G,过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE、BF相交于点H。
(1)图中有若干对三角形是全等的,请你任选一对进行证明。(不添加任何辅助线)
(2)证明:四边形AHBG菱形;
(3)若使四边形AHBG是正方形。还需在Rt△ABG的边长之间再添加一个什么条件?请你写出这个条件。(不必证明)

22.如图,点A是一个半径为

六、解答题(共3个小题,第23、24题各7分,第25 题8分,共22分)
23.小宇同学在布置班级文化园地时,想从一块长为
24.甲、乙两家公司共有150名工人,甲公司每名工人月工资为1200元.乙公司每名工人月工资为1500元。两家公司每月需付给工人工资共计19.5万元。
(1)求甲、乙公司分别有多少名工人;
(2)经营一段时向后发现,乙公司工人人均月产值是甲公司工人的3.2倍,于是甲公司决定内部调整。选拔了本公司部分工人到新的岗位工作。调整后,原岗位工人和新岗位工人的人均月产值分别为调整前的1.2倍和4倍,且甲公司新岗位工人的月生产总值不超过乙公司月生产总值的40%,甲公司的月生产总值不少于乙公司的月生产总值,求甲公司选拔到新岗位的工人有当少人?
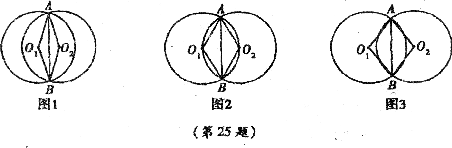
25.如图1、2、3是两个半径都等于2的⊙O1和⊙O2,由重合状态沿水平方向运动到互相外切过程中的三个位置,⊙O1和⊙O2相交于A、B两点,分别联结O
(1)如图2,当∠AO1B=120°时,求两圆重叠部分图形的周长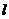 ;
;
(2)设∠AO1B的度数为 ,两圆重叠部分图形的周长为
,两圆重叠部分图形的周长为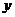 ,求
,求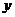 关于
关于 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(3)由(2),若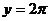 ,则线段O
,则线段O 的取值范围。
的取值范围。