1．已知⊙O的半径是5，A点为线段PO的中点，当OP=10时，点A与圆的位置关系是    (  )

    A．点A在圆内      B．点A在圆外          C．点A在圆上          D．不能确定

2．下列说法：(1)直径是弦；  (2)弦是直径；  (3)半圆是弧，但弧不一定是半圆；(4)半径相等的两个圆是等圆；  (5)长度相等的两条弧是等弧．其中错误的个数是    (    )

    A．1个       B．2个              C．3个              D．4个

3．在△ABC中，∠A、∠B均为锐角，且，则△ABC是    (    )

    A．等腰三角形     B．等边三角形         C．直角三角形         D．等腰直角三角形

4．若二次函数的图象如图所示，则a的值是    (    )

A．2             B．一2                C．±2         D．无法确定

5．如图，AB是⊙O的直径，C是AB延长线上一点，CD切⊙O于D，∠C=30°，CD=3cm，则AC的长为    (    )

A．cm         B．cm          C．cm         D．9cm

6．下面4个图是一根电线杆在一天中不同时刻的影长图，则按其一天中发生的先后顺序排列，正确的是    (    )

A．④①②③    B．④③①②    C．①②③④    D．④①③②

7．已知两圆的半径分别为R和r(R>r)，圆心距为d，且．则这两圆的位置关系是    (  )

    A．外切    B．内切            C．外离            D．外切或内切

8．已知二次函数，当取时，函数值相等，则当取时，函数值是    (  )

    A．a+c       B．a―c             C．―c          D．c

9．圆锥的侧面展开图是一个半圆，则这个圆锥的母线长与底面半径的比是  (    )

    A．2：1        B．2：l                C．：l           D．：1

10．在△ABC中，∠C=90°，∠A、∠B、∠C所对边长分别为a、b、c，则a³cosA+b³cosB  等于    (    )

    A．abc       B．(a+c)c²                C．c³                   D．ac²

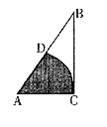
11．如图，在△ABC中，∠C=90°，∠A=60°，以A为圆心，AC长为半径画弧交AB于D．若扇形ACD的面积(阴影部分)为6cm²，则AB的长为    (  )

    A．6cm      B．12cm             C．6cm            D．6cm

12．如图，直线经过点M(3，0)，且平行于y轴，与抛物线交于点N，若S_△OMN=9，则a的值是    (    )

    A．        B．              C．                D．

13．一张桌子上摆放着若干个碟子，三种视图如图所示，则桌子上共有碟子  (    )

    A．6个       B．8个              C．12个            D．17个

14．圆内接正六边形的边长与该边所对的劣弧的长的比是    (    )

    A．1：        B．1：                 C．3：                 D．6：

15．路灯距地面8米，身高1．6米的小明从距离灯的底部(点O)20米的点A处，沿AO方向行走14米到点B时，人影长度    (    )

    A．变长2．5米    B．变长3．5米         C．变短2．5米         D．变短3．5米

16．将函数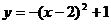的图象向          平移          个单位，得到函数的图象．

17．如图，一宽为2cm的刻度尺在圆上移动，当刻度尺的一边与圆相切时，另一边与圆两个交点处的读数恰好为2和8(单位：cm)，则该圆的半径为        cm．

18．已知二次函数，其中，当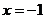时，y的值是        ．

19．如图，AB为⊙O的弦，∠AOB=100°，点C在⊙O上，且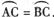，则∠CAB的度数为         ．

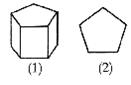
20．如图(1)表示一个正五棱柱形状的建筑物，如图(2)是它的俯视图，小明站在地面上观察该建筑物，当只能看到建筑物的一个侧面时，他的活动区域有          个．

21．在△ABC中，∠C=90°，tanB=，则cosA等于         ．

22．如图，⊙O的两条弦AB和CD相交于点P，∠B=30°，∠APD=80°，则∠A等于      ．

23．某校九年级科技小组利用日晷设计原理，设计制造了一台简易的“日晷”，并在一个阳光明媚的日子里记录了不同时刻晷针的影长，其中10：00时的影长被墨水污染：

    7：00  10cm    8：00  7.5cm    9：00  5.5cm   10：00  cm

    11：00  3cm    12：00  2.5cm

    请根据规律，判断10：00时，该晷针的影长是          cm．

24．如图，AB是半圆O的直径，延长AB至点C，使OB=BC，OC=4，点P是半圆上一动点(不与点A、点B重合)，∠ACP=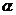，则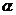的取值范围是                

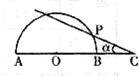
25．如图，两个相交的圆环的圆心分别为O₁，O₂，且O₁A=O₂A=3cm，O₁C=O₂D=2cm，四边形O₁AO₂B是正方形．则“8”字形(阴影部分)的面积是           ．

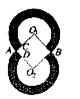
26．如图，⊙O是△ABC的外接圆，∠BAC=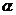，弦BC=sin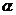，试探究⊙O的半径的值．

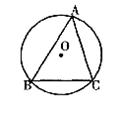
27．如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D是AB的延长线上的一点，AE⊥DC交DC的延长线于点E，且AC平分∠EAB．求证：DE是⊙O的切线．

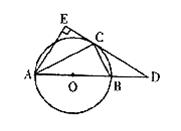
28．如图，一段街道的两边缘所在直线分别为AB、PQ，并且AB//PQ．建筑物的一端DE所在的直线MN⊥AB于点M，交PQ于点N．小亮从胜利街的A处，沿着AB方向前进，小明一直站在点P的位置等候小亮．

    (1)请你在图中画出小亮恰好能看见小明时的视线及此时小亮所在位置(用点C标出)；

    (2)若MN=20m，MD=8m，PN=24m，求(1)中的点C到胜利街口的距离CM．

29．如图，大楼高30m，附近有一座塔BC，某人在楼底A处测得塔顶的仰角为60°，爬到楼顶D处测得塔顶的仰角为30°，求塔高BC及大楼与塔之间的距离AC(结果精确到0．01m,参考数据：)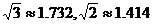

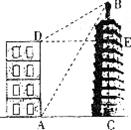
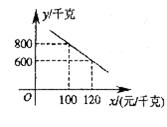
30．某海参养殖公司经市场调研发现，每周该公司销售的海参量y(千克)与单价(元/千克)之间存在如图所示的一次函数关系．

    (1)根据图象求y与之间的函数表达式；

    (2)从经济效益来看，你认为该公司如何制定海参单价，能使每周海参的销售收入最高?每周海参的最高销售收入是多少?

五、探索题：(满分16分)

31．已知抛物线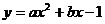经过点A(一1，0)、B(m，0)(m>0)，且与y轴交于点C

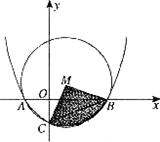
(1)求抛物线对应的函数表达式(用含m的式子表示)；

    (2)如图，⊙M经过A、B、C三点，求扇形MBC(阴影部分)的面积S(用含m的式子表示)；

    (3)若抛物线上存在点P，使得△APB∽△ABC，求m的值．