1．运算的结果是（    ）

A．－6              B．6                C．－9              D．9

2．下列图案属于轴对称图形的是（    ）

3．如图，这是一幅电热水壶的主视图，则它的俯视图是（    ）

4．如图，点A、B、C在⊙O上，∠ABC＝60°，则∠A0C的度数为（     ）

A．30°             B．60°             C．100°            D．120°

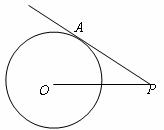
5．估计的值 （     ）                                             

A．在3到4之间     B．在4到5之间     C．在5到6之间     D．在6到7之间

6．如图，已知棋子“卒”的坐标为（－2，3），棋子“马”的坐标为（1，3），则棋子“炮”的坐标为（    ）

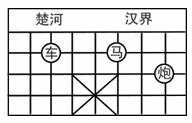
A．（3，2）          B．（3，1）          C．（2，2）          D．（－2，2）                                       

7．人民商场对上周女装的销售情况进行了统计，如下表所示：                                          

颜色

黄色

绿色

白色

紫色

红色

数量（件）

100

180

220

80

550

经理决定本周进女装时多进一些红色的，可用来解释这一现象的统计知识是（    ）

A．平均数           B．中位数           C．众数             D．方差

8．利用计算器求sin30°时，依次按键则计算器上显示的结果是（    ）

A．0．5             B．0．707           C．0．866           D．1

9．如图所示，把一个正方形对折两次后沿虚线剪下，展开后所得的图形是（    ）

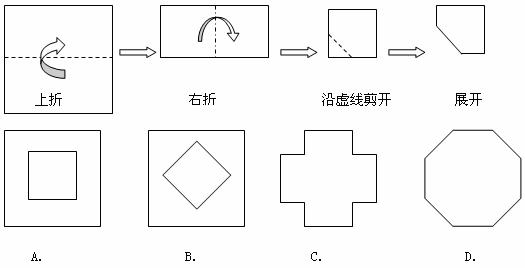
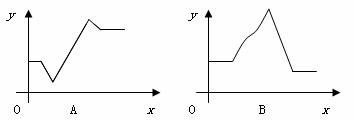
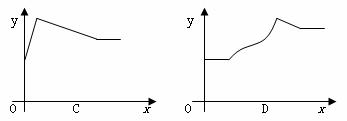
10．如图，乌鸦口渴到处找水喝，它看到了一个装有水的瓶子，但水位较低，且瓶口又小，乌鸦喝不着水，沉思一会后，聪明的乌鸦衔来一个个小石子放入瓶中，水位上升后，乌鸦喝到了水。在这则乌鸦喝水的故事中，设从乌鸦看到瓶的那刻起向后的时间为x，瓶中水位的高度为y，下列图象中最符合故事情景的是（    ）

试卷Ⅱ

（非选择题，共120分）

注意事项：

    1．试卷请用黑色、蓝色钢笔或圆珠笔直接作答。

    2．答题前将密封线内的项目填写清楚。

11．分解因式：－9＝                  。

12．使式子有意义的x的取值范围是                  。

13．地球上陆地面积约为149 000 000 km²，用科学记数法可以表示为               km²（保留三个有效数字）

14．菱形的两条对角线长分别是6和8，则菱形的边长为          。

15．如图，⊙O的半径为5，PA切⊙O于点A，∠APO＝30°，则切线长PA为               。（结果保留根号）

16．某一时刻，身高为165cm的小丽影长是55cm，此时，小玲在同一地  点测得旗杆的影长为5m，则该旗杆的高度为            m。

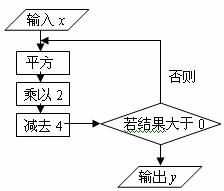
17．根据如图所示的程序计算，若输入x的值为1，则输出y的值为        。

18．如图，用火柴棒按以下方式搭小鱼，搭1条小鱼用8根火柴棒，搭2条小鱼用14根，……，则搭n条小鱼需要            根火柴棒。（用含n的代数式表示）

19．（本题8分）

    计算：

20．（本题8分）

    解不等式组，并把其解集在数轴上表示出来。

21．（本题8分）

    如图，点C、E、B、F在同一直线上，AC∥DF，AC＝DF，BC＝EF，△ABC与△DEF全等吗？证明你的结论。

22．（本题8分）

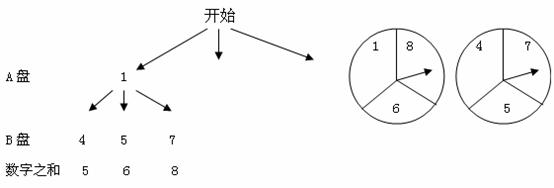
    如图，有两个可以自由转动的均匀转盘A、B，都被分成3等份，每份内均有数字，小明和小亮用这两个转盘做游戏，游戏规则如下：分别转动转盘A和B，两个转盘停止后，将两个指针所指份内的数字相加（如果指针恰好停在等分线上，那么重转一次，直到指针指向某一份为止），若和为偶数，则小明获胜；如果和为奇数，那么小亮获胜。

把下列树状图补充完整，并求小明获胜的概率。

    解：树状图为：

23．（本题9分）

    如图所示，小华设计了一个探究杠杆平衡条件的实验：在一根匀质的木杆中点O左侧固定位置B处悬挂重物A，在中点O右侧用一个弹簧秤向下拉，改变弹簧秤与点O的距离x（cm），观察弹簧秤的示数y（N）的变化情况。实验数据记录如下：

x（cm）

…

10

15

20

25

30

…

y（N）

…

30

20

15

12

10

…

（1）把上表中x，y的各组对应值作为点的坐标，在坐标系中描出相应的点，用平滑曲线连接这些点并观察所得的图象，猜测y（N）与x（cm）之间的函数关系，并求出函数关系式；  

（2）当弹簧秤的示数为24N时，弹簧秤与O点的距离是多少cm？随着弹簧秤与O点的距离不断减小，弹簧秤上的示数将发生怎样的变化？

24．（本题9分）

    为了解中学生的视力情况，某市有关部门采用抽样调查的方法从全市10万名中学生中抽查了部分学生的视力，分成以下四类进行统计：

    A．视力在4．2及以下                        B．视力在4．3～4．5之间

C．视力在4．6～4．9之间                        D．视力在5．0及以上

（1）这次抽查中，一共抽查了         名中学生；

（2）“类型D”在扇形图中所占的圆心角是           度；

（3）在统计图一中将“类型B”的部分补充完整；

（4）视力在5．0以下（不含5．0）均为不良，请估计全市视力不良的中学生人数。

25．（本题9分）

    某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作，已知该水果的进价为8元/千克，下面是他们在活动结束后的对话。

小丽：如果以10元/千克的价格销售，那么每天可售出300千克。

小强：如果以13元/千克的价格销售，那么每天可获取利润750元。

小红：通过调查验证，我发现每天的销售量y（千克）与销售单价x（元）之间存在一次函数关系。

（1）求y（千克）与x（元）（x＞0）的函数关系式；

（2）设该超市销售这种水果每天获取的利润为W元，那么当销售单价为何值时，每天可获得的利润最大？最大利润是多少元？【利润＝销售量×（销售单价－进价）】

26．（本题12分）

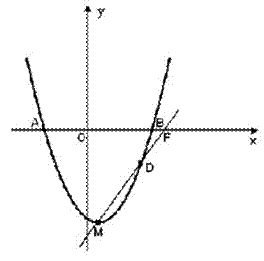
    如图，已知抛物线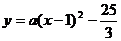与x轴交于A、B两点（点A在左边），且过点D（5，－3），顶点为M，直线MD交x轴于点F。

（1）求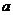的值；

（2）以AB为直径画⊙P，问：点D在⊙P上吗？为什么？

（3）直线MD与⊙P存在怎样的位置关系？请说明理由。

27．（本题12分）

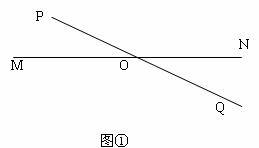
操作：如图①，点O为线段MN的中点，直线PQ与MN相交于点O，请利用图①画出一对以点O为对称中心的全等三角形。

                                                                                      根据上述操作得到的经验完成下列探究活动：

探究一：如图②，在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE＝∠EAF，AF与DC的延长线相交于点F。试探究线段AB与AF、CF之间的等量关系，并证明你的结论；

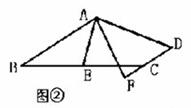
探究二：如图③，DE、BC相交于点E，BA交DE于点A，且BE：EC＝1：2，

∠BAE＝∠EDF，CF∥AB。若AB＝5，CF＝1，求DF的长度。

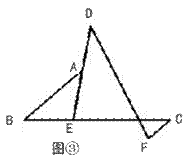
28．（本题13分）

如图，矩形EFGH的边EF＝6cm，EH＝3cm，在平行四边形ABCD中，BC＝10cm，AB＝5cm，sin∠ABC＝，点E、F、B、C在同一直线上，且FB＝1cm，矩形从F点开始以1cm/s的速度沿直线FC向右运动，当边GF所在直线到达D点时即停止。

（1）在矩形运动过程中，何时矩形的一边恰好通过平行四边形ABCD的边AB或CD的中点？

（2）若矩形运动的同时，点Q从点C出发沿C－D－A－B的路线，以cm/s的速度运动，矩形停止时点Q也即停止运动，则点Q在矩形一边上运动的时间为多少s？

（3）在矩形运动过程中，当矩形与平行四边形重叠部分为五边形时，求出重叠部分面积S（）与运动时间t（s）之间的函数关系式，并写出时间t的范围。是否存在某一时刻，使得重叠部分的面积S＝16．5？若存在，求出时间t，若不存在，说明理由。