网址:http://m.1010jiajiao.com/timu_id_685157[举报]
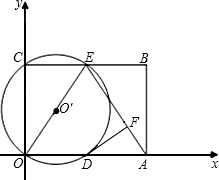 如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.(1)求OA、OC的长;
(2)求证:DF为⊙O′的切线;
(3)小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由. 查看习题详情和答案>>
(本题12分) 如图,在平行四边形ABCD中,AB在x轴上,D点y轴上,![]() ,
,![]() ,B点坐标为(4,0).点
,B点坐标为(4,0).点![]() 是边
是边![]() 上一点,且
上一点,且![]() .点
.点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,以1厘米/秒的速度分别沿
同时出发,以1厘米/秒的速度分别沿![]() 、
、![]() 向点
向点![]() 运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为
运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为![]() ,设运动时间为
,设运动时间为![]() 秒。
秒。
(1)求直线BC的解析式。
(2)当![]() 为何值时,
为何值时,![]() ?
?
(3)在(2)问条件下,⊙E与直线PF是否相切;如果相切,加以证明,并求出切点的坐标。如果不相切,说明理由。
查看习题详情和答案>>
(本题满分10分)
![]() 、
、![]() 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往![]() 城,乙车驶往
城,乙车驶往![]() 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距![]() 城高速公路入口处的距离
城高速公路入口处的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (时)之间的关系如图.
(时)之间的关系如图.

1.(1)求![]() 关于
关于![]() 的表达式;
的表达式;
2.(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,相遇前两车相距的路程为![]() (千米).请直接写出
(千米).请直接写出![]() 关于
关于 的表达式;
的表达式;
3.(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为![]() (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度![]() .在下图中画出乙车离开
.在下图中画出乙车离开![]() 城高速公路入口处的距离
城高速公路入口处的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (时)之间的函数图象.
(时)之间的函数图象.
查看习题详情和答案>>
(本题满分12分)
已知直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.

1.(1)填空:菱形ABCD的边长是 ▲ 、面积是 ▲ 、 高BE的长是 ▲ ;
2.(2)探究下列问题:
若点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上时
② △APQ的面积S关于t的函数关系式,以及S的最大值;
3.(3)在运动过程中是否存在某一时刻使得△APQ为等腰三角形,若存在求出t的值;若不存在说明理由.
查看习题详情和答案>>
(本题满分8分)先阅读读短文,再解答短文后面的问题:
![]() 在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向。在线段的两个端点中(如图),如果我们规定一个顺序:
在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向。在线段的两个端点中(如图),如果我们规定一个顺序:![]() 为始点,
为始点,![]() 为终点,我们就说线段
为终点,我们就说线段![]() 具有射线的
具有射线的![]() 方向,线段
方向,线段![]() 叫做有向线段,记作
叫做有向线段,记作![]() ,线段
,线段![]() 的长度叫做有向线段
的长度叫做有向线段![]() 的长度(或模),记作
的长度(或模),记作![]() 。
。
有向线段包含三个要素:始点、方向和长度,知道了有向线段的始点,它的终点就被方向和长度一确定。解答下列问题:

1.(1)在平面直角坐标系中画出有向线段![]() (有向线段与
(有向线段与![]() 轴的长度单位相同),
轴的长度单位相同),![]() ,
,![]() 与
与![]() 轴的正半轴的夹角是
轴的正半轴的夹角是![]() ,且与
,且与![]() 轴的正半轴的夹角是
轴的正半轴的夹角是![]() ;
;
2.(2)若![]() 的终点
的终点![]() 的坐标为(3,
的坐标为(3,![]() ),求它的模及它与
),求它的模及它与![]() 轴的正半轴的夹角
轴的正半轴的夹角![]() 的度数。
的度数。
查看习题详情和答案>>