2007-2008学年度烟台市海阳第一学期期中考试
九年级数学试题
一、选择题（本题共12个小题，每小题4分，共计48分）下列每小题均给出标号为A、B、C、D的四个备选答案，只有一个是正确的。
1．
的值等于
A．
B．
C．
D．1
2．在Rt△ABC中，∠C=90°，AC=，AB=2，则∠A等于
A．30° B．45° C．60° D．90°
3．如图，将一长为
A．
B．
C．
D．
4．如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，已知BC=
，
，则CD的长可表示为
A．
B．
C．
D．
5．在函数
中，自变量
的取值范围是
A．
B．
C．
D．
6．二次函数
图像如图所示，则点A（ac，bc）在
A．第一象限 B．第二象限 C．第三象限 D．第四象限
7．已知二次函数
的最大值为0，则
A．
，
B．
，
C．， D．，
8．如图所示，二次函数的图像经过点（－1，2），且与轴交点的横坐标分别为
，
，其中
，
，下列结论：
①
； ②
； ③
； ④
其中正确的有
A．1个 B．2个 C．3个 D．4个
9．二次函数
的图像可能是
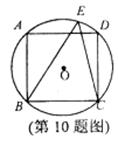
10．如图，正方形ABCD内接于⊙D，点E在劣弧AD上，则∠BEC等于
A．45° B．60° C．30° D．55°
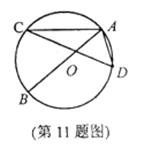
11．如图，AB是⊙O的直径，∠ACD=15°，则∠BAD等于
A．75° B．72° C．70° D．65°
12．已知：点P到直线
的距离为3，以点P为圆心，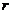
为半径画圆，如果圆上有且只有两点到直线的距离均为2，则半径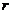的取值范围是
A．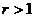
B．
C．
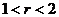D．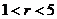
二、填空题：（本题共6个小题，每小题4分，共计24分）
13．当太阳光与地面成55°角时，直立于地面的玲玲测得自己的影长为l
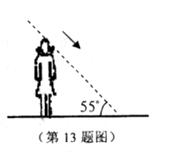
14．写出一个图像最高点为（－1，0）的二次函数的表达式__________________。
15．在Rt△ABC中，∠ACB=90°，
，则
的值为_________。
16．如图，已知AB是⊙D的直径，弦CD⊥AB，AC
，BC=1，那么sin∠BCD的值是_________。
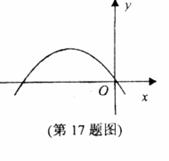
17．如图所示的抛物线是二次函数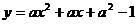
的图像，且过原点O，那么该抛物线与轴的另一个交点的坐标是_________。
18．⊙O的直径AB为
三、解答题（本题满分l6分，第19、20题各8分）
19．已知：如图，AB是⊙O的弦，点C在弧AB上
（1）若∠OAB=35°，求∠AOB的度数；
（2）过点C作CD∥AB，若CD是⊙O的切线，求证：点C是弧AB的中点。
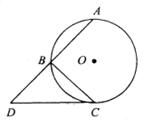
20．如图，AB，BC是⊙O的两条弦，且BC⊥AB，延长AB至D，使BD=AB，连接DC。当弦AB与BC满足什么关系时，DC为⊙O的切线？证明你的结论。
四、解答题（本题满分8分）
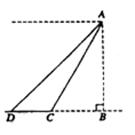
21．如图，从山顶A处看到地面C点的俯角为60°，看到地面D点的俯角为45°，测得
米，求山高AB。（精确到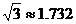
）
五、解答题（本题满分8分）
22．如图，山脚下有一棵大树AB，小华从点A沿着山坡向上走
，
，
，
，
，
）
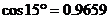六、解答题（本题满分l0分）
23．已知对称轴平行于
轴的一抛物线与轴的交点是A（－2，0）、B（1，0），且经过点C（2，－8）。
（1）求该抛物线的解析式；
（2）求该抛物线的顶点坐标。
七、解答题（本题满分l0分）
24．如图，P是⊙O外一点，PA，PB分别与⊙O相切于点A，B，点C是弧AB上一点，经过点C作⊙O的切线，分别与PA，PB相交于点D，E，∠DOE=75°。
（1）求∠P的度数；
（2）若AD=
八、解答题（本题满分l2分）
25．在某次樱桃节前夕，某果品批发公司为指导今年的樱桃销售，对往年的市场销售情况进行了调查统计，得到如下数据：
销售价（元／千克）
…
25
24
23
22
…
销售量（千克）
…
2000
2500
3000
3500
…
（1）在平面直角坐标系内，作出各组有序数对（，）所对应的点，连接各点并观察所得的图形，判断与之间的函数关系，并求出与之间的函数关系式；
（2）若樱桃进价为l3元／千克，试求销售利润P（元）与销售价（元／千克）之间的函数关系式。当销售价为多少时，可获得最大销售利润，最大利润是多少元？
九、解答题（本题满分l4分）
26．已知点M、N的坐标分别为（0，1）、（0，－1），点P是抛物线
上的一个动点，过点N作平行于轴的直线。
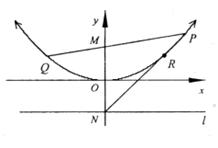
（1）求证：以点P为圆心，PM为半径的团与直线相切；
（2）设直线PM，NP与抛物线的另一个交点分别为点Q，R，求证：Q，R两点关于轴对称．