2006-2007学年度潍坊市诸城九年级下学期
单元过关考(五)
第Ⅰ卷(选择题,共36分)
一、选择题(将正确答案的代号填在题后括号内,每小题3分,共36分)
1.下列运算正确的是( )
A.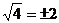 B.
B.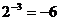 C.
C.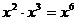 D.
D.
2.某物体的三视图是如图所示的三个图形,那么该物体形状是( )

A.长方体 B.立方体 C.圆柱体 D.圆锥体
3.一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是( )
A.14 B.15 C.16 D.17

A.0.96小时 B.1.07小时 C.1.15小时 D.1.50小时
5.有2名男生和2名女生,王老师要随机地、两两一对地为他们排座位,一男一女排在一起的概率是( )
A.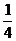 B.
B. C.
C. D.
D.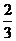
6.为了奖励进步较大的学生,某班决定购买甲、乙、丙三种钢笔作为奖品,其单价分别为4元、5元、6元,购买这些钢笔需要花60元;经过协商,每种钢笔单价下降1元,结果只花了48元,那么甲种钢笔可能购买( )
A.11支 B.9支 C.7支 D.5支
7.如图,在矩形ABCD中,EF//AB,GH//BC,EF、GH的交点P在BD上,图中面积相等的四边形有( )
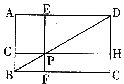
A.3对 B.4对 C.5对 D.6对
8.小华同学自制了一个简易的幻灯机,其工作情况如图所示,幻灯片与屏幕平行,光源到幻灯片的距离是30cm,幻灯片到屏幕的距离是l5cm,幻灯片上小树的高度是10cm,则屏幕上小树的高度是( )
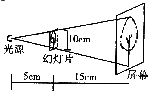
A.50cm B.500cm C.60cm D.600cm
9.如图,已知点A的坐标为(1,0),点B在直线y=-x上运动,当线段AB最短时,点B的坐标为( )

A.(0,0) B.( ,
,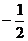 )
C.(
)
C.( ,
,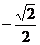 ) D.(
) D.(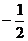 ,
, )
)
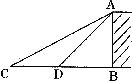
10.如图为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进l2m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB的高度等于( )
A. B.
B.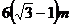 C.
C.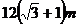 D.
D.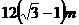
11.已知圆锥侧面展开图的圆心角为90°,则该圆锥的底面半径与母线长的比为( )
A.1:2 B.2:1 C.1:4 D.4:1
12.已知二次函数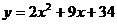 ,当自变量
,当自变量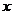 取两个不同的值
取两个不同的值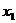 ,
,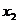 时,函数值相等,则当自变量
时,函数值相等,则当自变量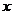 取
取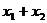 时的函数值与( )
时的函数值与( )
A.x=1时的函数值相等 B.x=0时的函数值相等
C.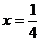 时的函数值相等 D.
时的函数值相等 D. 时的函数值相等
时的函数值相等
第Ⅱ卷(非选择题,共84分)
二、填空题(每小题3分,共18分)
13.台湾是我国最大的岛屿,总面积为35989.76平方千米,这个数据用科学记数法表示为___________平方千米(保留两个有效数字).
14.关于x的不等式3x一2a≤一2的解集如图所示,则a的值是__________.

15.直线y=k?4与y轴相交所成的锐角的正切值为 ,则k的值为___________.
,则k的值为___________.
16.某校抽查了50名九年级学生对艾滋病三种主要传播途径的知晓情况,结果如下表:估计该校九年级550名学生中,三种传播途径都知道的有___________人.
传播途径(种)
0
1
2
3
知晓人数(人)
3
7
15
25
17.如右图中的螺旋形由一系列等腰直角三角形组成,其序号依次为①、②、③、④、⑤……,则第n个等腰直角三角形的斜边长为_____________.

18.下图是一单位拟建的大门示意图,上部是一段直径为l0米的圆弧形,下部是矩形ABCD,其中AB=3.7米,BC=6米,则AD的中点到BC的距离是________.

三、解答题:(共7小题,共66分)
19.(10分)我市部分学生参加了2007年全国初中数学竞赛决赛,并取得优异成绩.已知竞赛成绩分数都是整数,试题满分为l40分,参赛学生的成绩分数分布情况如下:
分数段
0―19
20一39
40―59
60一79
80―99
100―119
120―l40
人数
0
37
68
95
56
32
12
请根据以上信息解答下列问题:
(1)全市共有多少人参加本次数学竞赛决赛?最低分和最高分在什么分数范围?
(2)经竞赛组委会评定,竞赛成绩在60分以上(含60分)的考生均可获得不同等级的奖励,求我市参加本次竞赛决赛考生的获奖比例;
(3)决赛成绩分数的中位数落在哪个分数段内?
(4)上表还提供了其他信息,例如:“没获奖的人数为l05人”等等.请你再写出两条此表提供的信息.
20.(8分)一条东西走向的高速公路上有两个加油站A、B,在A的北偏东45°方向还有一个加油站C,C到高速公路的最短距离是30千米,B、C间的距离是60千米。想要经过C修一条笔直的公路与高速公路相交,使两路交叉口P到B、C的距离相等,请求出交叉口P与加油站A的距离(结果可保留根号).
21.(8分)为加强公民节约用水,减少污水排放的环保意识,某城市制定了以下用水收费标准(含城市污水处理费):每户每月用水未超过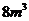 时,按1.2元/
时,按1.2元/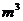 收费;每户每月用水超过
收费;每户每月用水超过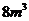 时,其中
时,其中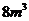 仍按原标准收费,超过部分按1.9元/
仍按原标准收费,超过部分按1.9元/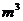 收费.设某户每月用水量为
收费.设某户每月用水量为 ,应交水费为y(元).
,应交水费为y(元).
(1)分别写出用水量未超过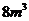 和超过
和超过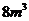 时,y与x之间的函数关系式;
时,y与x之间的函数关系式;
(2)某用户五月份共交水费l3.4元,问该用户五月份用水多少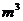
22.(8分)任意剪一个三角形纸片,如图中的△ABC,不妨设它的一个锐角为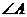 ,首先利用对折的方法得到高AN。然后按图中所示的方法分别将含有
,首先利用对折的方法得到高AN。然后按图中所示的方法分别将含有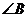 、
、 的部分向里折,找出AB、AC的中点D、E,同时得到两条折痕DF、EG,分别沿折痕DF、EG剪下图中的三角形①,②,并按图中箭头所指的方向分别旋转180°。
的部分向里折,找出AB、AC的中点D、E,同时得到两条折痕DF、EG,分别沿折痕DF、EG剪下图中的三角形①,②,并按图中箭头所指的方向分别旋转180°。
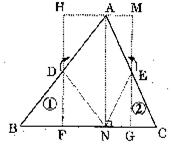
(1)你能拼成一个什么样的四边形?并说明你的理由;
(2)请你利用这个图形,证明三角形的面积公式:S=底高。
23.(10分)如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米。点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么
(1)设△POQ的面积为y,求y关于t的函数解析式;
(2)当△POQ的面积最大时,将△POQ沿直线PQ翻折后得到△PCQ,试判断点C是否落在直线AB上,并说明理由;
(3)当t为何值时,△POQ与△AOB相似.

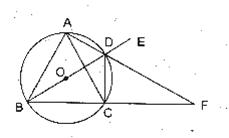
24.(10分)如图,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC延长线于F,DE是BD的延长线,连结CD.
(1)求证: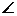 EDF=
EDF=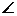 CDF;
CDF;
(2)求证: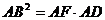 ;
;
(3)若BD正好是⊙O的直径,且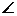 EDC=120°,BC=6cm,求AF的长.
EDC=120°,BC=6cm,求AF的长.
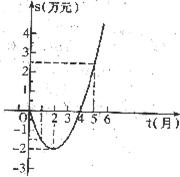
25.(12分)为了顺应市场要求,我市某花炮厂技术部研制开发一种新产品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图像(部分)刻画了该厂年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系)根据图象提供的信息,解答下列问题:
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末花炮厂累积利润可达到30万元?
(3)求第8个月公司所获利润是多少万元?