2007年滨州市博兴县中考模拟试题(二)
数学试题
一、选择题:(本题有10小题,共30分。每小题只有一个选项是正确的,不选、多选、错选均不给分)
1.小马虎在下面的计算中只做对了一道题,他做对的题目是
A.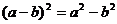 B.
B.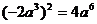
C.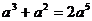 D.
D.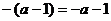
2.如图1是小明用八块小正方体搭的积木,该几何体的俯视图是

3.一件衣服标价132元,若以9折降价出售,仍可获利l0%,则这件衣服的进价是
A.106元 B.105元 C.118元 D.108元
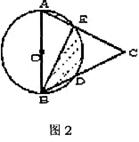
4.如图2,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C。若CE=2,则图中阴影部分的面积是
A.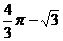 B.
B.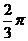
C.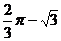 D.
D.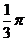
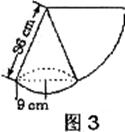
5.小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作圆锥形的生日礼帽。如图3,圆锥帽底半径为
A.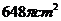 B.
B.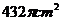 C.
C.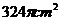 D.
D.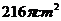
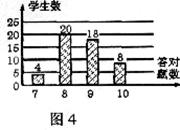
6.数学老师布置10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成条形统计图(如图4),根据此图可知,每位同学答对的题数所组成样本的中位数和众数分别为
A.8,8 B.8.
7.已知矩形的面积为l0,则它的长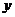 与宽
与宽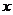 之间的关系用图像大致可表示为
之间的关系用图像大致可表示为
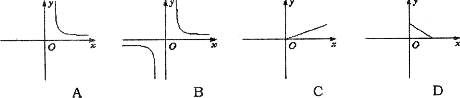
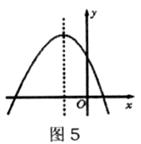
8.已知二次函数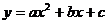 的图像如图5所示,则在“①
的图像如图5所示,则在“①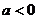 ,②
,②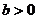 ,③
,③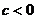 ,④
,④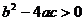 ”中正确的判断是
”中正确的判断是
A.①②③④ B.④ C.①②③ D.①④
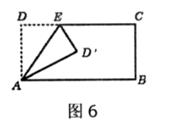
9.将矩形ABCD沿AE折叠,得到如图6所示的图形,已知∠CED=60°。则∠AED的大小是
A.60° B.50° C.75° D.55°
10.若“!”是一种数学运算符号,并且l !=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则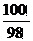 的值为
的值为
A.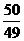 B.99! C.9900 D.2!
B.99! C.9900 D.2!
二、填空题(本大题共8小题,每小题4分,共32分)
11.某公司成立3年以来,积极向国家上缴利税,由第一年的200万元增长到800万元,则平均每年增长的百分数是_________。
12.不等式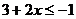 的解集是_________。
的解集是_________。
13.小芳画一个有两边长分别为5cm和6 cm的等腰三角形,则这个等腰三角形的周长是_________。
14.如图,在边长为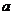 的正方形中剪去一个边长为
的正方形中剪去一个边长为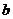 的小正方形(
的小正方形(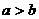 ),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式_________________。
),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分的面积,验证了公式_________________。
15.两个变量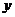 与
与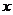 之间的函数图像如图所示,则
之间的函数图像如图所示,则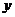 的取值范围是__________________。
的取值范围是__________________。
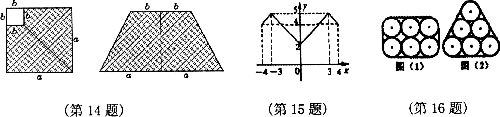
16.图(1)、图(2)是两种方法把6根圆形钢管用钢丝捆扎的截面图。设图(1)、图(2)两种方法捆扎所需钢丝绳的长度是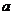 、
、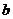 (不记接头部分),则
(不记接头部分),则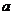 、
、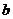 的大小关系为:
的大小关系为: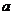 _________
_________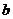 (填“<”、“=”或“>”)。
(填“<”、“=”或“>”)。
17.点M既在一次函数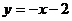 的图像上,又在反比例函数
的图像上,又在反比例函数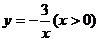 的图像上,则M点的坐标是_________。
的图像上,则M点的坐标是_________。
18.下图是一组数据的折线统计图,这组数据的极差是_________,平均数是_________。
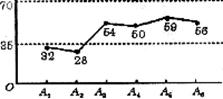
三、解答题(本题有7个小题,共58分)
19.(本小题5分)
解方程: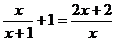
20.(本小题7分)
某校需要添置某种教学仪器,有两种方案:
方案l:到商家购买,每件需要8元;
方案2:学校自己制作,每件4元,另外需要制作工具的租用费l20元。
设需要仪器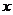 件,方案1与方案2的费用分别为
件,方案1与方案2的费用分别为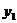 ,
, (元)。
(元)。
(1)分别写出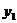 ,
, 的函数表达式;
的函数表达式;
(2)当购置仪器多少件时,两种方案的费用相同?
(3)需要仪器50件,采用哪种方案便宜?请说明理由。
21.(本小题8分)
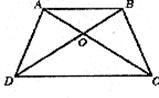
如图,在四边形ABCD中,对角线AC、BD相交于点O,
已知∠ADC=∠BCD,AD=BC,求证:DO=CO。
22.(本小题8分)
有一个抛两枚硬币的游戏,规则是:若出现两个正面,则甲赢;若出现一正一反,则乙赢;若出现两个反面,则甲、乙都不赢。
(1)这个游戏是否公平?请说明理由;
(2)如果你认为个游戏不公平,那么请你改变游戏规则,设计一个公平的游戏;如果你认为这个游戏公平,那么请你改变游戏规则,设计一个不公平的游戏。
23.(本小题8分)
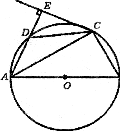
如图,四边形ABCD内接于⊙O,AB是⊙O的直径,CE切⊙O于点C,AE⊥CE,且交⊙O 于点D。
求证:(1)DC=BC;(2)BC2=AB?DE.
24.(本小题10分)
某自行车厂今年生产销售一种新型自行车,现向你提供以下有关的信息:
(1)该厂去年已备有这种自行车车轮l0000只,车轮车间今年平均每月可生产车轮1500只,每辆自行车需装配2只车轮;
(2)该厂装配车间(自行车最后一道工序的生产车间)每月至少可装配这种自行车l 000辆,但不超过l 200辆:
(3)该厂已收到各地客户今年订购这种自行车14500辆的订货单;
(4)这种自行车出厂销售单价为500元/辆。
设该厂今年这种自行车的销售金额为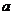 万元。请你根据上述信息,判断
万元。请你根据上述信息,判断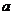 的取值范围是多少?
的取值范围是多少?
25.(本小题12分)
正方形ABCD的边长为4,P是BC上一动点,QP⊥AP交DC于Q,设PB=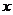 ,△ADQ的面积为
,△ADQ的面积为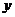 。
。
(1)求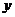 与
与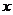 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量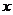 的取值范围。
的取值范围。
(2)(1)中函数若是一次函数,求出直线与两坐标轴围成的三角形面积,若是二次函数,请利用配方法求出抛物线的对称轴和顶点坐标。
(3)画出这个函数的图像。
(4)点P是否存在这样的位置,使△APB的面积是△ADQ的面积的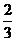 ,若存在,求出BP的长,若不存在,说明理由。
,若存在,求出BP的长,若不存在,说明理由。