2007年滨州市中等学校招生统一考试
数学试题
温馨提示:
1.请将密封线内的各项目填写清楚,把座号填在第2页右下角的座号栏内.
2.本试卷共10页,试题满分为120分,考试时间为120分钟.
一、填空题:本大题共l0小题,每小题3分,共30分.把答案填在题中横线上.
1.0.000328用科学记数法表示(保留二个有效数字)为
2.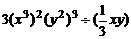 =
=
3.若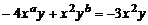 ,贝
,贝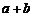 =
=
4.钟表在整点时,时针与分针的夹角会出现5种度数相等的情况,请分别写出它们的度数
5.数据6,8,8, 的众数有两个,则这组数据的中位数是
的众数有两个,则这组数据的中位数是
6.第三象限内的点P( ,
,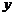 ),满足
),满足 ,则点P的坐标是
,则点P的坐标是
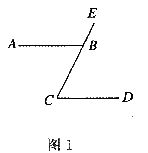
7.如图1所示,AB∥CD,∠ABE=110°,则∠ECD=
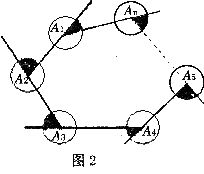
8.如图2所示,分别以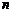 边形的顶点为圆心,以单位l为半径画圆,则图中阴影部分的面积之和为
个平方单位.
边形的顶点为圆心,以单位l为半径画圆,则图中阴影部分的面积之和为
个平方单位.
9.如图3所示,每个小方格都是边长为1的正方形,点A、B是方格纸的两个格点(即正方形的顶点),在这个6×6的方格纸中,找出格点C,使△ABC的面积为1个平方单位的直角三角形的个数是
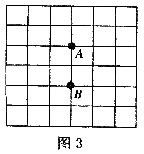
10.如图4表示“龟兔赛跑”时路程与时间的关系,已知龟、兔上午8:O0从同一地点出发,请你根据图中给出的信息,算出乌龟在 点追上兔子.
二、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.请把选出的答案的字母标号填在题后的括号内.
11.对角线互相垂直平分的四边形是( ).
(A)平行四边形、菱形 (B)矩形、菱形 (C)矩形、正方形 (D)菱形、正方形
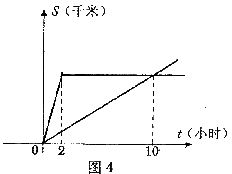
12.关于 的一元二次方程
的一元二次方程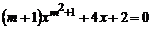 的解为( ).
的解为( ).
(A)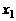 =1,
=1,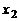 =-1 (B)
=-1 (B)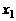 =
=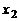 =1
(C)
=1
(C) 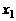 =
=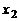 =-1 (D)无解
=-1 (D)无解
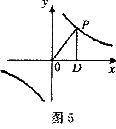
13.如图5,点P为反比例函数)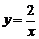 上的一动点,作PD⊥
上的一动点,作PD⊥ 轴于点D,△POD的面积为
轴于点D,△POD的面积为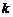 ,则函数
,则函数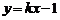 的图象为( ).
的图象为( ).

 14.如图6,在Rt△ABC中,∠C=90°,AC=3.将其绕B点顺时针旋转一周,则分别以BA、BC为半径的圆形成一圆环.该圆环的面积为( ).
14.如图6,在Rt△ABC中,∠C=90°,AC=3.将其绕B点顺时针旋转一周,则分别以BA、BC为半径的圆形成一圆环.该圆环的面积为( ).
(A)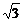
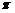 (B)3
(B)3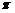 (C)9
(C)9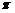 (D)6
(D)6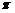
 15.如图7,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( ).
15.如图7,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( ).
(A)sinA的值越大,梯子越陡
(B)cosA的值越大,梯子越陡
(C)tanA的值越小,梯子越陡
(D)陡缓程度与∠A的函数值无关
16.―矩形硬纸板绕其竖直的一边旋转l80°所形成的几何体的主视图和俯视图分别为( )
 (A)矩形,矩形
(B)圆,半圆 (C)圆,矩形 (D)矩形,半圆
(A)矩形,矩形
(B)圆,半圆 (C)圆,矩形 (D)矩形,半圆
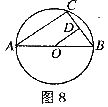
17.如图8,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( ).
 (A)
(A) cm
(B)3cm
cm
(B)3cm
(C)5cm (D)6cm
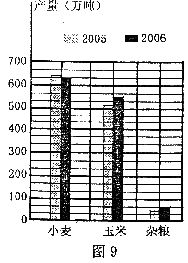
18.如图9,这是某地2005年和2006年粮食作物产量的条形统计图,请你根据此图判断下列说法合理的是( ).
(A)2006年三类农作物的产量比2005年都有增加
(B)玉米产量和杂粮产量增加的幅度大约是一样的
(C)2005年杂粮产量是玉米产量的约六分之一
(D)2005年和2006年的小麦产量基本持平
三、解答题:本大题共8小题,满分66分.解答应写出文字说明、证明过程或推演步骤.
19.(本小题满分5分)
先化简,再求值: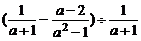 ,其中
,其中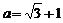 :
:
20.(本小题满分6分)
解方程: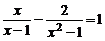
21.(本小题满分7分)
解不等式组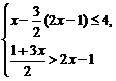 把解集表示在数轴上,并求出不等式组的整数解
把解集表示在数轴上,并求出不等式组的整数解
22.(本小题满分10分)
(1)把二次函数 化成
化成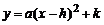 的形式.
的形式.
(2)写出抛物线 的顶点坐标和对称轴,并说明该抛物线是由哪一条形如
的顶点坐标和对称轴,并说明该抛物线是由哪一条形如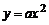 的抛物线经过怎样的变换得到的?
的抛物线经过怎样的变换得到的?
(3)如果抛物线 中,
中, 的取值范围是0≤
的取值范围是0≤ ≤3,请画出图象,并试着给该抛物线编一个具有实际意义的情境(如喷水、掷物、投篮等).
≤3,请画出图象,并试着给该抛物线编一个具有实际意义的情境(如喷水、掷物、投篮等).
23.(本小题满分8分)
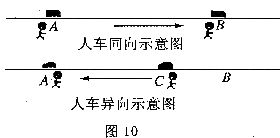
某人在电车路轨旁且与路轨平行的路上骑车行走,他留意到每隔6分钟有一部电车从他后面驶向前面,每隔2分钟有一部电车从对面驶向后面.假设电车和此人行驶的速度都不变(分别用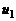 、
、 表示),请你根据下面的示意图,求电车每隔几分钟(用t表示)从车站开出一部?
表示),请你根据下面的示意图,求电车每隔几分钟(用t表示)从车站开出一部?
24.(本小题满分10分)
如图11,在△ABC和△DEF中,∠A=∠D=90°,AB=DE=3,AC=2DF=4.
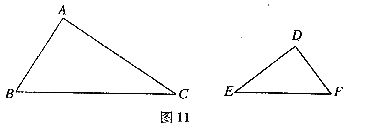
(1)判断这两个三角形是否相似?并说明为什么?
(2)能否分别过A、D在这两个三角形中各作一条辅助线,使△ABC分割成的两个三角形与△DEF分割成的两个三角形分别对应相似?证明你的结论.
25.(本小题满分8分)
我市长途客运站每天6:30―7:30开往某县的三辆班车,票价相同,但车的舒适程度不同.小张和小王因事需在这一时段乘车去该县,但不知道三辆车开来的顺序.两人采用不同的乘车方案:小张无论如何决定乘坐开来的第一辆车,而小王则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.若第二辆车的状况比第一辆车好,他就上第二辆车;若第二辆车不如第一辆车,他就上第三辆车。若按这三辆车的舒适程度分为优、中、差三等,请你思考并回答下列问题:
(1)三辆车按出现的先后顺序共有哪几种可能?
(2)请列表分析哪种方案乘坐优等车的可能性大?为什么?
26.(本小题满分l2分)
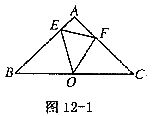
如图l2―1所示,在△ABC中,AB=AC=2,∠A=90°,O为BC的中点,动点E在BA边上自由移动,动点F在AC边上自由移动.
(1)点E、F移动的过程中,△OEF是否能成为∠EOF=45°的等腰三角形?若能,请指出△OEF为等腰三角形时动点E、F的位置.若不能,请说明理由.
(2)当∠EOF=45°时,设BE= ,CF=
,CF=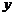 ,求
,求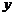 与
与 之间的函数解析式,写出
之间的函数解析式,写出 的取值范围.
的取值范围.
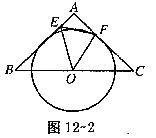
(3)在满足(2)中的条件时,若以O为圆心的圆与AB相切(如图l2―2),试探究直线EF与⊙O的位置关系,并证明你的的结论.