2007年临沂市初中毕业与高中招生考试
数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至4页,第Ⅱ卷5至12页.满分120分.考试时间120分钟.
第Ⅰ卷(选择题 共42分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案.不能答在试卷上.
3.考试结束,将本试卷和答题卡一并交回.
一、选择题(本大题共14小题,每小题3分,共42分)在每小题所给的四个选项中,只有一项是符合题目要求的.
1. 的绝对值是( )
的绝对值是( )
A. B.
B.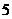 C.
C.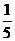 D.
D.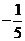
2.据了解,我市每年用于校舍维护维修的资金约需7300万元,用科学记数法表示这一数据为( )
A.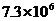 元 B.
元 B.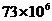 元 C.
元 C.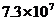 元 D.
元 D.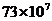 元
元
3.下列运算正确的是( )
A.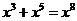 B.
B.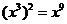 C.
C.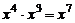 D.
D.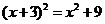
4.如图,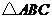 中,
中,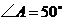 ,点
,点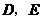 分别在
分别在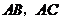 上,则
上,则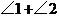 的大小为( )
的大小为( )
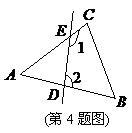 A.
A.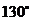 B.
B.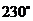 C.
C.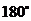 D.
D.
5.计算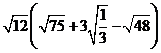 的结果是( )
的结果是( )
A.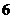 B.
B.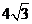 C.
C.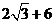 D.
D.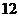
6.如图表示一个用于防震的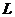 形的包装用泡沫塑料,当俯视这一物体时看到的图形形状是( )
形的包装用泡沫塑料,当俯视这一物体时看到的图形形状是( )
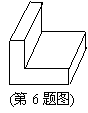 |
|||
 |
|||
7.若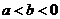 ,则下列式子:
,则下列式子:
①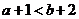 ;
;
②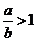 ;
;
③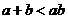 ;
;
④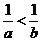 中,正确的有( )
中,正确的有( )
A.1个 B.2个 C.3个 D.4个
8.已知反比例函数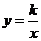 的图象在第二、四象限内,函数图象上有两点
的图象在第二、四象限内,函数图象上有两点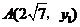 ,
,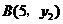 ,则
,则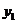 与
与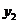 的大小关系为( )
的大小关系为( )
A.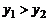 B.
B.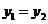 C.
C.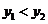 D.无法确定
D.无法确定
9.直线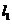 :
: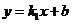 与直线
与直线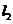 :
: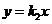 在同一平面直角坐标系中的图象如图所示,则关于
在同一平面直角坐标系中的图象如图所示,则关于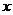 的不等式
的不等式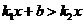 的解为( )
的解为( )
A.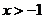 B.
B.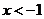 C.
C.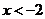 D.无法确定
D.无法确定
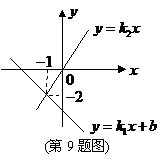 |
|||
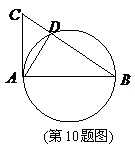 |
|||
10.如图,在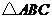 中,
中,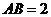 ,
,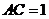 ,以
,以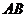 为直径的圆与
为直径的圆与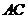 相切,与边
相切,与边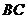 交于点
交于点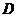 ,则
,则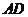 的长为( )
的长为( )
A.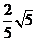 B.
B.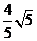 C.
C.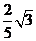 D.
D.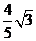
11.如图,矩形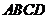 中,
中,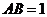 ,
,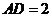 ,
,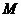 是
是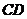 的中点,点
的中点,点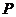 在矩形的边上沿
在矩形的边上沿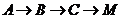 运动,则
运动,则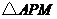 的面积
的面积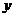 与点
与点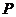 经过的路程
经过的路程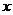 之间的函数关系用图象表示大致是下图中的( )
之间的函数关系用图象表示大致是下图中的( )
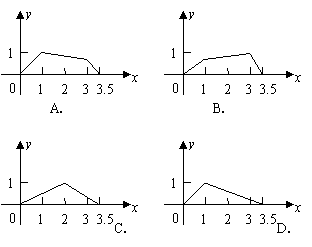 |
|||
 |
|||
12.小明随机地在如图所示的正三角形及内部区域投针,则针扎到其内切圆(阴影)区域的概率为( )
 A.
A.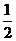 B.
B.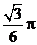
C.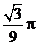 D.
D.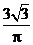
13.如图,客轮在海上以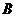 向
向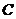 航行,在
航行,在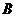 处测得灯塔
处测得灯塔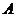 的方位角为北偏东
的方位角为北偏东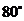 ,测得
,测得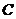 处的方位角为南偏东
处的方位角为南偏东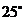 ,航行1小时后到达
,航行1小时后到达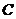 处,在
处,在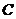 处测得
处测得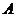 的方位角为北偏东
的方位角为北偏东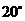 ,则
,则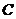 到
到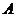 的距离是( )
的距离是( )
 A.
A.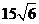 km
B.
km
B.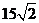 km C.
km C.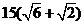 km D.
km D.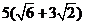 km
km
 |
14.如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中所示的方法从这些边角料上截取矩形(阴影部分)铁皮备用,当截取的矩形面积最大时,矩形两边长 应分别为( )
应分别为( )
A.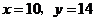 B.
B.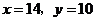
C.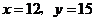 D.
D.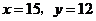
第Ⅱ卷(非选择题 共78分)
注意事项:
1.第Ⅱ卷共8页,用钢笔或圆珠笔直接答在试卷上.
2.答卷前将密封线内的项目及座号填写清楚.
二、填空题(本大题共5小题,每小题3分,共15分)把答案填在题中横线上.
15.计算: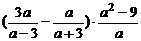 =
.
=
.
16.从数字1,2,3中任取两个不同数字组成一个两位数,则这个两位数大于21的概率是 .
17.如图,在四边形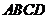 中,
中,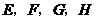 分别是
分别是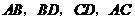 的中点,要使四边形
的中点,要使四边形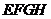 是菱形,四边形
是菱形,四边形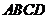 还应满足的一个条件是
.
还应满足的一个条件是
.
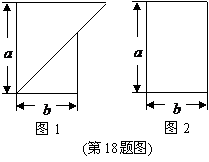 |
|||
 |
|||
18.有如图所示的两种广告牌,其中图1是由两个等腰直角三角形构成的,图2是一个矩形,从图形上确定这两个广告牌面积的大小关系,并将这种大小关系用含字母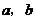 的不等式表示为
.
的不等式表示为
.
19.如果一个数等于它的不包括自身的所有因数之和,那么这个数就叫完全数.例如,6的不包括自身的所有因数为1,2,3.而且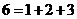 ,所以6是完全数.大约2200多年前,欧几里德提出:如果
,所以6是完全数.大约2200多年前,欧几里德提出:如果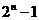 是质数,那么
是质数,那么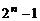 ?(
?(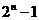 )是一个完全数,请你根据这个结论写出6之后的下一个完全数是
.
)是一个完全数,请你根据这个结论写出6之后的下一个完全数是
.
三、开动脑筋,你一定能做对!(本大题共3小题,共20分)
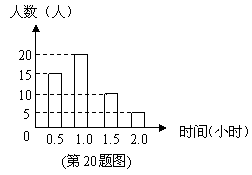
21.(本小题满分6分)
“种粮补贴”惠农政策的出台,大大激发了农民的种粮积极性,某粮食生产专业户去年计划生产小麦和玉米共18吨,实际生产了20吨,其中小麦超产12%,玉米超产10%,该专业户去年实际生产小麦、玉米各多少吨?
22.(本小题满分8分)
如图,已知矩形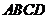 .
.
(1)在图中作出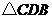 沿对角线
沿对角线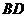 所在的直线对折后的
所在的直线对折后的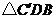 ,
,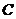 点的对应点为
点的对应点为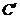 (用尺规作图,保留清晰的作图痕迹,简要写明作法);
(用尺规作图,保留清晰的作图痕迹,简要写明作法);
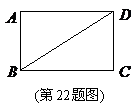 (2)设
(2)设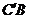 与
与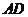 的交点为
的交点为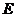 ,若
,若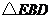 的面积是整个矩形面积的
的面积是整个矩形面积的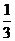 ,求
,求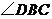 的度数.
的度数.
四、认真思考,你一定能成功!(本大题共2小题,共19分)
23.(本小题满分9分)
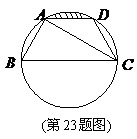 如图,已知点
如图,已知点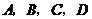 均在已知圆上,
均在已知圆上,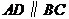 ,
,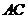 平分
平分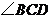 ,
,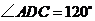 ,四边形
,四边形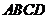 的周长为
的周长为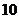 .
.
(1)求此圆的半径;
(2)求图中阴影部分的面积.
24.(本小题满分10分)
某工程机械厂根据市场需求,计划生产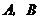 两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:
两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:
型号
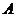
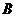
成本(万元/台)
200
240
售价(万元/台)
250
300
(1)该厂对这两型挖掘机有哪几种生产方案?
(2)该厂如何生产能获得最大利润?
(3)根据市场调查,每台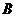 型挖掘机的售价不会改变,每台
型挖掘机的售价不会改变,每台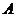 型挖掘机的售价将会提高
型挖掘机的售价将会提高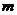 万元(
万元(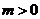 ),该厂应该如何生产可以获得最大利润?(注:利润=售价-成本)
),该厂应该如何生产可以获得最大利润?(注:利润=售价-成本)
五、相信自己,加油呀!(本大题共2小题,共24分)
25.(本小题满分11分)
如图1,已知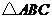 中,
中,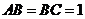 ,
, ,把一块含
,把一块含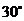 角的直角三角板
角的直角三角板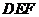 的直角顶点
的直角顶点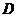 放在
放在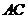 的中点上(直角三角板的短直角边为
的中点上(直角三角板的短直角边为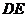 ,长直角边为
,长直角边为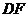 ),将直角三角板
),将直角三角板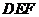 绕
绕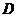 点按逆时针方向旋转.
点按逆时针方向旋转.
(1)在图1中,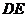 交
交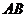 于
于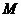 ,
,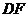 交
交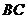 于
于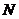 .
.
①证明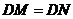 ;
;
②在这一旋转过程中,直角三角板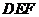 与
与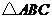 的重叠部分为四边形
的重叠部分为四边形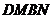 ,请说明四边形
,请说明四边形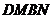 的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;
的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;
(2)继续旋转至如图2的位置,延长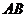 交
交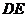 于
于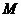 ,延长
,延长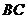 交
交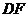 于
于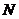 ,
,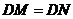 是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)继续旋转至如图3的位置,延长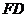 交
交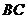 于
于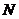 ,延长
,延长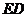 交
交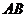 于
于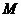 ,
,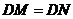 是否仍然成立?请写出结论,不用证明.
是否仍然成立?请写出结论,不用证明.
 |
26.(本小题满分13分)
如图1,已知抛物线的顶点为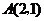 ,且经过原点
,且经过原点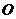 ,与
,与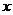 轴的另一个交点为
轴的另一个交点为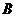 .
.
(1)求抛物线的解析式;
(2)若点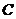 在抛物线的对称轴上,点
在抛物线的对称轴上,点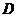 在抛物线上,且以
在抛物线上,且以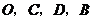 四点为顶点的四边形为平行四边形,求
四点为顶点的四边形为平行四边形,求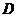 点的坐标;
点的坐标;
(3)连接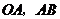 ,如图2,在
,如图2,在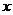 轴下方的抛物线上是否存在点
轴下方的抛物线上是否存在点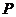 ,使得
,使得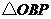 与
与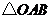 相似?若存在,求出
相似?若存在,求出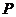 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
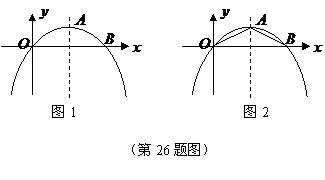 |