(3)连接.如图2.在轴下方的抛物线上是否存在点.使得与相似?若存在.求出点的坐标,若不存在.说明理由．——青夏教育精英家教网——

摘要：(3)连接.如图2.在轴下方的抛物线上是否存在点.使得与相似?若存在.求出点的坐标,若不存在.说明理由．

网址：http://m.1010jiajiao.com/timu_id_671552[举报]

如图，在平面直角坐标系中，已知点B（-2

，0），A（m，0）（-

＜m＜0），以AB为边在x轴下方作正方形ABCD，点E是线段OD与正方形ABCD的外接圆除点D以外的另一个交点，连接BE与AD相交于点F．
（1）求证：BF=DO；
（2）设直线l是△BDO的边BO的垂直平分线，且与BE相交于点G．若G是△BDO的外心，试求经过B、F、O三点的抛物线的解析表达式；
（3）在（2）的条件下，在抛物线上是否存在点P，使该点关于直线BE的对称点在x轴上？若存在，求出所有这样的点的坐标；若不存在，请说明理由．查看习题详情和答案>>

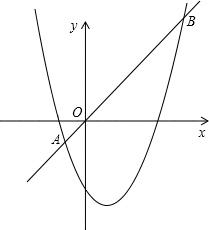
如图，在平面直角坐标系中，抛物线y=x²-2x-4与直线y=x交于点A、B，M是抛物线上一个动点，连接OM．
（1）当M为抛物线的顶点时，求△OMB的面积；
（2）当点M在抛物线上，△OMB的面积为10时，求点M的坐标；
（3）当点M在直线AB的下方且在抛物线对称轴的右侧，M运动到何处时，△OMB的面积最大．

查看习题详情和答案>>

如图，在平面直角坐标系中，二次函数y=x²+bx+c的图象与x轴交于A（-

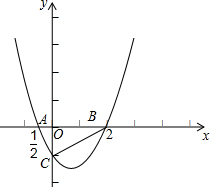B（2，0），且与y轴交于点C．
（1）求该抛物线的解析式，并判断△ABC的形状；
（2）点P是x轴下方的抛物线上一动点，连接PO，PC，并把△POC沿CO翻折，得到四边形POP′C，求出使四边形POP′C为菱形的点P的坐标；
（3）在此抛物线上是否存在点Q，使得以A，C，B，Q四点为顶点的四边形是直角梯形？若存在，求出Q点的坐标；若不存在，说明理由．查看习题详情和答案>>

如图，在平面直角坐标系中，以A（3，0）为圆心，以5为半径的圆与x轴相交于B、C，与y轴的负半轴相交于D．
（1）若抛物线y=ax²+bx+c经过B、C、D三点，求此抛物线的解析式，并写出抛物线与圆A的另一个交点E的坐标；
（2）若动直线MN（MN∥x轴）从点D开始，以每秒1个长度单位的速度沿y轴的正方向移动，且与线段CD、y轴分别交于M、N两点，动点P同时从点C出发，在线段OC上以每秒2个长度单位的速度向原点O运动，连接PM，设运动时间为t秒，当t为何值时，

的值最大，并求出最大值；
（3）在（2）的条件下，若以P、C、M为顶点的三角形与△OCD相似，求实数t的值．

查看习题详情和答案>>

如图①，在平面直角坐标系中，Rt△AOB≌Rt△CDA，且A（-1，0）、B（0，2），抛物线y=ax²+ax-2经过点C．
（1）求抛物线的解析式；
（2）在抛物线（对称轴的右侧）上是否存在两点P、Q，使四边形ABPQ是正方形？若存在，求点P、Q的坐标，若不存在，请说明理由；
（3）如图②，E为BC延长线上一动点，过A、B、E三点作⊙O′，连接AE，在⊙O′上另有一点F，且AF=AE，AF交BC于点G，连接BF．下列结论：①BE+BF的值不变；②

，其中有且只有一个成立，请你判断哪一个结论成立，并证明成立的结论．

查看习题详情和答案>>