2006年大连市初中毕业升学统一考试
数 学
本试卷1~8页,共150分,考试时间120分钟。
请考生准备好圆规,直尺、三角板、计算器等答题工具.
一、选择题(本题8小题,每小题3分,共24分)
 说明:将下列各题唯一正确的答案代号A、B、C、D填到题后的括号内。
说明:将下列各题唯一正确的答案代号A、B、C、D填到题后的括号内。
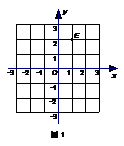
1.如图1,在平面直角坐标系中,点E的坐标是 ( )
A.(1, 2) B.(2, 1) C.(-1, 2) D.(1,-2)
2.在△ABC中,∠C = 90°,AC = 3,BC = 4,则sinA的值是 ( )
 A.
A.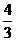 B.
B.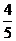 C.
C. D.
D.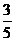
3.如图2,Rt△ABC∽Rt△DEF,则∠E的度数为 ( )
A.30° B.45° C.60° D.90°
4.下列各式运算结果为x4的是 ( )
A.x4?x4 B.(x4)
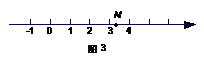 5.小伟五次数学考试成绩分别为:86分、78分、80分、85分、92分,
5.小伟五次数学考试成绩分别为:86分、78分、80分、85分、92分,
李老师想了解小伟数学学习变化情况,则
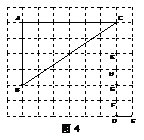 小伟数学成绩的 ( )
小伟数学成绩的 ( )
A.平均数 B.众数 C.中位数 D.方差
6.如图3,数轴上点N表示的数可能是 ( )
A.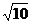 B.
B.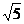 C.
C.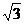 D.
D.
7.如图4,点A、B、C、D、E、F、G、H、K都是7×8方格纸
中的格点,为使△DEF∽△ABC,则点M应是F、G、H、K
四点中的 ( )
8.图5能折叠成的长方体是 ( )

二、填空题(本题共7小题,每小题3分,共21分)
 说明:将答案直接填在题后的横线上。
说明:将答案直接填在题后的横线上。
9.-2的绝对值等于____________.
10.某水井水位最低时低于水平面
水平面
 11.已知两圆的圆心距O1O2为3,⊙O1的半径为1,⊙O2的半径为2,
11.已知两圆的圆心距O1O2为3,⊙O1的半径为1,⊙O2的半径为2,
则⊙O1与⊙O2的位置关系为____________________.
12.如图6,点P是⊙O外一点,PA切⊙O于点A,
∠O = 60°,则∠P度数为__________________.
13.大连某小区准备在每两幢楼房之间,开辟面积为300平方米
 的一块长方形绿地,并且长比宽多
的一块长方形绿地,并且长比宽多
为x米,则可列方程为_____________________________.
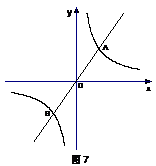
14.如图7,双曲线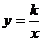 与直线
与直线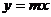 相交于A、B两点,
相交于A、B两点,
B点坐标为(-2,-3),则A点坐标为_______________.
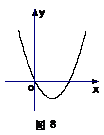
15.图8是二次函数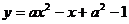 的图象,则a的值是____________.
的图象,则a的值是____________.
三、解答题(本题共5小题,其中16、17题各9分,18、19、20题各10分, 共48分)
16.已知方程 的解是k,求关于x的方程
的解是k,求关于x的方程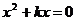 的解.
的解.
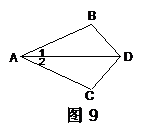 17.如图9,已知∠1 = ∠2,AB = AC. 求证:BD = CD
17.如图9,已知∠1 = ∠2,AB = AC. 求证:BD = CD
(要求:写出证明过程中的重要依据)
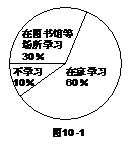 18.某社区要调查社区居民双休日的学习状况,采用下列调查方式:
18.某社区要调查社区居民双休日的学习状况,采用下列调查方式:
①从一幢高层住宅楼中选取200名居民;
②从不同住宅楼中随机选取200名居民;
③选取社区内200名在校学生.
⑴上述调查方式最合理的是_____________________;
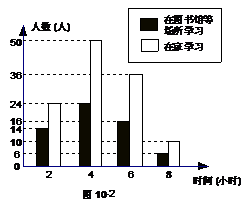 ⑵将最合理的调查方式得到的数据制成扇形统计图(如图10-1)和频数分布直方图(如图10-2).在这个调查中,200名居民双休日在家学习的有____________人;
⑵将最合理的调查方式得到的数据制成扇形统计图(如图10-1)和频数分布直方图(如图10-2).在这个调查中,200名居民双休日在家学习的有____________人;
⑶请估计该社区2 000名居民双休日学习时间
不少于4小时的人数.
19.如图11,点O、B坐标分别为(0, 0)、(3, 0),将△OAB绕O点按逆时针方向旋转
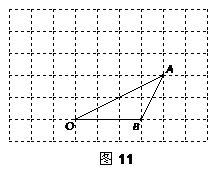 90°到OA′B′;
90°到OA′B′;
⑴画出△OA′B′;
⑵点A′的坐标为________________;
⑶求BB′的长.
20.小明为了检验两枚六个面分别刻有点数1、2、3、4、5、6的正六面体骰子的质量是否都合格,在相同的条件下,同时抛两枚骰子20 000次,结果发现两个朝上面的点数和是7的次数为20次.你认为这两枚骰子质量是否都合格(合格标准为:在相同条件下抛骰子时,骰子各个面朝上的机会相等)?并说明理由.
四、解答题(本题共3小题,其中21题7分,22、23题各8分,共23分)
21.早晨小欣与妈妈同时从家里出发,步行与骑自行车到方向相反的两地上学与上班,图12是他们离家的路程 y (米)与时间 x (分)的函数图象.妈妈骑车走了10分时接到小欣的电话,即以原速骑车前往小欣学校,并与小欣同时到达学校.已知小欣步行速度为每分
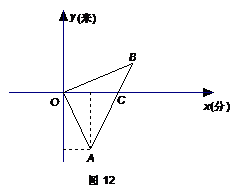 求小欣家与学校距离及小欣早晨上学需要的时间.
求小欣家与学校距离及小欣早晨上学需要的时间.
22.甲、乙两工程队分别承担一条
⑴求甲、乙两队完成任务需要的时间(用含x、y的代数式表示);
⑵问甲、乙两队哪队先完成任务?
23.如图13-1、图13-2分别是两个相同正方形、正六边形,其中一个正多边形的顶点在另一个正多边形外接圆圆心O处.
⑴求图13-1中,重叠部分面积与阴影部分面积之比;
⑵求图13-2中,重叠部分面积与阴影部分面积之比(直接出答案);
⑶根据前面探索和图13-3,你能否将本题推广到一般的正n边形情况,(n为大于2的偶数)?若能,写出推广问题和结论;若不能,请说明理由.

五、解答题和附加题(本题共3小题,24、25题各12分,26题10分,共34分,附加题5分,全卷累积不超过150分,附加题较难,建议考生最后答附加题)
24.小明为了通过描点法作出函数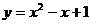 的图象,先取自变量x的7个值满足:
的图象,先取自变量x的7个值满足:
x2-x1 = x3-x2 = … = x7-x6 = d,再分别算出对应的y值,列出表1:
表1:
x
x1
x2
x3
x4
x5
x6
x7
y
1
3
7
13
21
31
43
记m1 = y2-y1,m2 = y3-y2,m3 = y4-y3,m4 = y5-y4,…;s1 = m2-m1,s2 = m3-m2,
s3 = m4-m3,…
⑴判断s1、s2、s3之间关系,并说明理由;
⑵若将函数“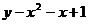 ”改为“
”改为“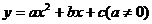 ”,列出表2:
”,列出表2:
表2:
x
x1
x2
x3
x4
x5
x6
x7
y
y1
y2
y3
y4
y5
y6
y7
其他条件不变,判断s1、s2、s3之间关系,并说明理由;
⑶小明为了通过描点法作出函数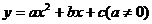 的图象,列出表3:
的图象,列出表3:
表3:
x
x1
x2
x3
x4
x5
x6
x7
y
10
50
110
190
290
412
550
由于小明的粗心,表3中有一个y值算错了,请指出算错的y值(直接写答案).
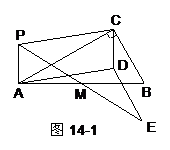 25.如图14-1,P为Rt△ABC所在平面内任意一点(不在直线
25.如图14-1,P为Rt△ABC所在平面内任意一点(不在直线
AC上),∠ACB = 90°,M为AB边中点.
操作:以PA、PC为邻边作平行四边形PADC,连续PM并
延长到点E,使ME = PM,连结DE.
探究:⑴请猜想与线段DE有关的三个结论;
⑵请你利用图14-2,图14-3选择不同位置的点P按上述方法操作;
⑶经历⑵之后,如果你认为你写的结论是正确的,请加以证明;
如果你认为你写的结论是错误的,请用图14-2或图14-3加以说明;
(注意:错误的结论,只要你用反例给予说明也得分)
⑷若将“Rt△ABC”改为“任意△ABC”,其他条件不变,利用图14-4操作,并写出与线
段DE有关的结论(直接写答案).
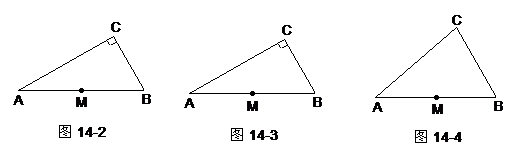
26.如图15,点P(-m,m2)抛物线:y = x2上一点,将抛物线E沿x轴正方向平移
若能,求点C的坐标;若不能,请说明理由.
说明:⑴如果你反复探索,没有解决问题,请写出探索过程(要求至少写3步);⑵在你完成⑴之后,可以从①、②中选取一个条件,完成解答(选取①得7分;选取②得10分).
①m = 1;②m = 2.
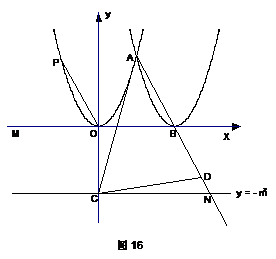
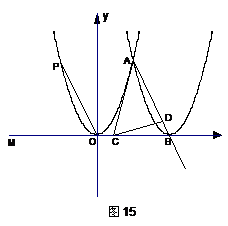 附加题:如图16,若将26题“点C是x轴上点B左侧一动点”改为“点C是直线y =-m2上点N左侧一动点”,其他条件不变,探究26题中的问题.
附加题:如图16,若将26题“点C是x轴上点B左侧一动点”改为“点C是直线y =-m2上点N左侧一动点”,其他条件不变,探究26题中的问题.