2006-2007学年济南市市中区九年级第一学期
期末数学试题
(满分:120分 考试时间:120分钟)
2007.1
一、选择题(本大题共10分,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.下列方程是一元二次方程的是( )
A. 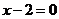 B.
B.  C.
C. 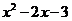 D.
D. 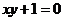
2.反比例函数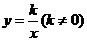 的图像经过点(2,5),则
的图像经过点(2,5),则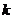 等于( )
等于( )
A. 10 B. 5 C. 2 D. 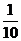
3.如图, 是
是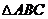 的外接圆,
的外接圆,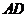 是
是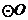 的直径,连接
的直径,连接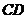 ,
,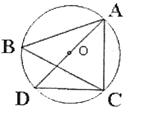
若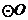 的半径
的半径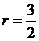 ,
,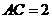 ,则
,则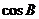 的值是( )
的值是( )
A. 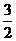 B.
B. 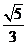 C.
C. 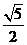 D.
D. 
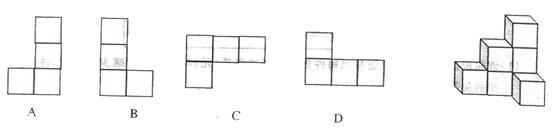
4.我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图,从图的左面看这个几何体的左视图是 ( )
5.如图, 在
在 上,
上,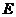 在
在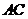 上,且
上,且 ,那么补充下列一个条件后,
,那么补充下列一个条件后,
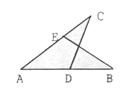 仍无法判定
仍无法判定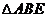 ≌
≌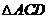 的是
的是
A. 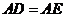
B. 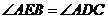
C. 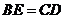
D. 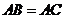
6.越来越多的商品房空置是目前比较突出的问题,据国家有关部门统计:2006年第一季度全国商品房空置面积达1.23亿平方米,比2005年第一季度增长23.8%,下列说法:
①
2005年第一季度全国商品房空置面积为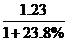 亿平方米。
亿平方米。
②
2005年第一季度全国商品房空置面积为 亿平方米。
亿平方米。
③
若按相同的增值率计算,2007年第一季度全国商品房空置面积达到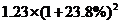 亿平方米。
亿平方米。
④
如果2007年第一季度全国商品房面积比2006年第一季度减少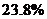 ,那么2007年第一季度全国商品房空置面积与2005年第一季度相同。
,那么2007年第一季度全国商品房空置面积与2005年第一季度相同。
其中正确的是( )
 A.
①④ B.②④ C.②③ D. ①③
A.
①④ B.②④ C.②③ D. ①③
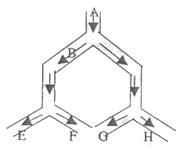
7.如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
A. 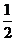 B.
B. 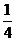 C.
C.  D.
D. 
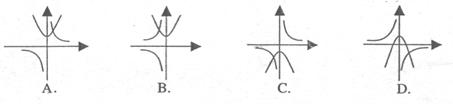
8.函数与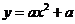 与
与 在同一直角坐标系中的图像可能是( )
在同一直角坐标系中的图像可能是( )
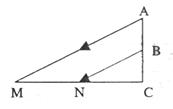 9.如图是一束平行的光线从教室窗户射入教室的平面示意图,测得光线与地面所成的角,窗户的高在教室地面上的影长MN=
9.如图是一束平行的光线从教室窗户射入教室的平面示意图,测得光线与地面所成的角,窗户的高在教室地面上的影长MN=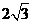 米,窗户的下檐到教室地面的距离BC=1米(点M,N,C在同一直线上),则窗户的高AB为( )
米,窗户的下檐到教室地面的距离BC=1米(点M,N,C在同一直线上),则窗户的高AB为( )
A. 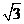 米 B. 3米
米 B. 3米
C. 2米 D.1.5米
10.如图,抛物线的函数表达式是( )
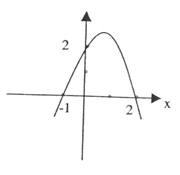 A.
A.
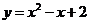
B. 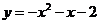
C. 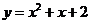
D. 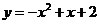
二、填空题(本大题共6小题,每小题3分,共18分,请把正确答案填写在下面的横线上)
11.命题“如果三角形有一个内角是钝角则其余两个内角都是锐角”的逆命题是
,它是 (填“真”或“假”)命题。
12.半径为5cm的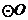 中,30°的圆周角所对的弦等于
cm
中,30°的圆周角所对的弦等于
cm
13.已知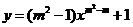 是二次函数,则
是二次函数,则 =
。
=
。
14.顺次连结任意四边形各边中点所得到的四边形一定是 形。
15.已知等腰三角形内接于半径为5的 中,如果底边BC的长为6,则底角的正切值为
中,如果底边BC的长为6,则底角的正切值为
。
16.已知半径为5和r的两个圆相切,如果圆心距为8,那么r= 。
三、解答题(本大题共11小题,共72分,解答应写出文字说明或演算步骤)
17.(本题5分)计算: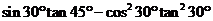
18.(本题6分)若0是关于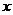 的方程的
的方程的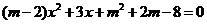 的解,求实数
的解,求实数 的值。
的值。
19.(本题6分)如图,在平地上有两棵树,已知,某一时刻它们的影长正好等于树的各自的高度,请你画出此时产生树影的光线及其影子。(请你在作图时标注必要的角度)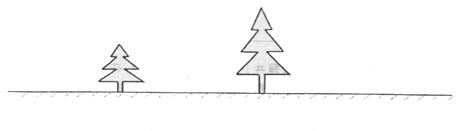
20.(本题6分)某种新产品进价是120元,在试销阶段发现每件售价(元)与产品的销售量(件)始终存在下表中的数量关系:
每件售价(元)
130
150
165
每日销售量(件)
70
50
35
(1)请你根据商场所给数据写出每件售价提高的数量(元)与日销售量减少的数量(件)之间的关系;
(2)在不改变上述关系的情况下,请你帮助商场经理策划每件商品定价为多少元时,每日盈利可达到1600元?
21.(本题6分)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球试验,将球搅匀后从中随即摸出一只球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数
100
150
200
500
800
1000
摸到白球的次数
58
96
116
295
484
601
摸到白球的频率
0.58
0.64
0.58
0.59
0.605
0.601
(1)请估计:当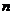 很大时,摸到白球的频率将会接近
。
很大时,摸到白球的频率将会接近
。
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 。
(3)试估算口袋中黑、白两种颜色的球各有多少只?
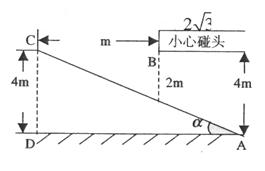 22.(本题7分)济南某大型超市为方便顾客购物,准备在一至二楼之间安装电梯,如图,楼顶与地面平行,要是身高2m以下的人在笔直站立的情况下搭乘电梯,在B处不碰到头部,请你帮超市设计,电梯与一楼地面的夹角
22.(本题7分)济南某大型超市为方便顾客购物,准备在一至二楼之间安装电梯,如图,楼顶与地面平行,要是身高2m以下的人在笔直站立的情况下搭乘电梯,在B处不碰到头部,请你帮超市设计,电梯与一楼地面的夹角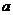 最小为多少度?
最小为多少度?
 23.(本题6分)新安商厦对销售量较大的A、B、C三种品牌的洗衣粉进行了问卷调查,发放问卷270份(问卷由单选和多选题组成)。对收回的238份问卷进行了在整理,部分数据如下:
23.(本题6分)新安商厦对销售量较大的A、B、C三种品牌的洗衣粉进行了问卷调查,发放问卷270份(问卷由单选和多选题组成)。对收回的238份问卷进行了在整理,部分数据如下:
内容
质量
广告
价格
品牌
A
B
C
A
B
C
A
B
C
满意户数
194
121
117
163
172
107
98
96
100
根据上述信息回答下列问题:
(1) A品牌洗衣粉的主要竞争优势是什么?你是怎样看出来的?
(2) 广告对用户选择品牌有影响吗?请简要说明理由。
(3) 你对A厂家有何建议?
二、用户对各品牌洗衣粉满意情况汇总表:
24.(本题6分)已知一次函数 的图像与反比例函数
的图像与反比例函数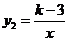 的图像相交,其中一个交点的纵坐标为6。
的图像相交,其中一个交点的纵坐标为6。
(1)求两个函数的表达式:
(2)结合图像求出时,的取值范围。
25.(本题7分)如图,现有一横截面积是一抛物线型的水渠。一次,水渠管理员将一根长1.5m的标杆一端放在水渠底部的A点,另一端露出水面并靠在水渠边缘的B点,发现标杆有1m浸没在水中,露出水面部分的标杆与水面成30°的夹角(标杆与抛物线的横截面在同一平面内)。
(1)如图,以水面所在直线为轴,以过底部的中心A且垂直于水平面的直线为轴建立直角坐标系,求该水渠横截面抛物线的表达式。
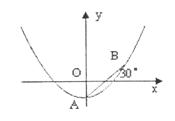 (2)在(1)的条件下,求当水面再上升0.3m时的水面宽约为多少?(取2.24,结果精确到0.1m)
(2)在(1)的条件下,求当水面再上升0.3m时的水面宽约为多少?(取2.24,结果精确到0.1m)
26.(本题8分)如图,已知AB是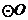 的直径,直线CD与
的直径,直线CD与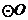 相切于点C,AC平分
相切于点C,AC平分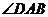 。
。
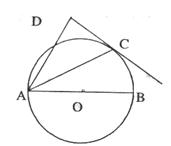 (1)问:AD与DC垂直吗?为什么?
(1)问:AD与DC垂直吗?为什么?
(2)若AD=2,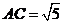 ,求AB的长。
,求AB的长。
27.(本题9分)问题背景:某课外学习小组在一次学习研讨中,得到了如下两个命题:
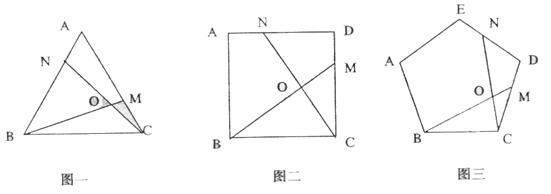
Ⅰ.如图一,在正三角形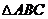 中,M、N分别是AC、AB上的点,BM与CN相交于点O,若
中,M、N分别是AC、AB上的点,BM与CN相交于点O,若 , 则BM=CN。
, 则BM=CN。
Ⅱ.如图二,在正三角形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若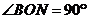 ,则BM=CN。
,则BM=CN。
任务要求:
(1) 请你从Ⅰ、Ⅱ两个命题中选择一个进行证明。
(2) 如图,在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若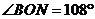 ,请问结论BM=CN是否还成立?若成立,请予以证明;若不成立,请说明理由。
,请问结论BM=CN是否还成立?若成立,请予以证明;若不成立,请说明理由。