2006年泰安市中等学校招生考试(课改区)
第Ⅰ卷
一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记零分)
1.我国对农村义务教育阶段贫困家庭的学生实行“两免一补”政策,2005年至2007年三年内国家财政将安排约 亿元资金用于“两免一补”,这项资金用科学记数法表示为( )
亿元资金用于“两免一补”,这项资金用科学记数法表示为( )
A.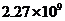 元 B.
元 B. 元
元
C.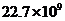 元 D.
元 D.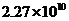 元
元
2.下列运算正确的是( )整式的运算
A.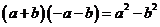 B.
B.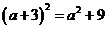
C.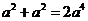 D.
D.
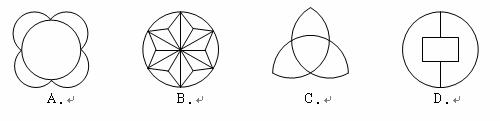
3.下列轴对称图形中,对称轴最多的是( )轴对称
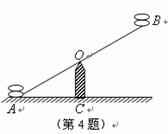
4.如图,是跷跷板示意图,横板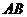 绕中点
绕中点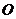 上下转动,立柱
上下转动,立柱 与地面垂直,当横板
与地面垂直,当横板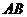 的
的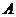 端着地时,测得
端着地时,测得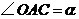 ,则在玩跷跷板时,上下最大可以转动的角度为( )
,则在玩跷跷板时,上下最大可以转动的角度为( )
A. B.
B.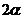 C.
C. D.
D.
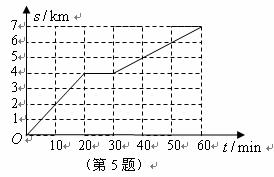
5.如图,是一同学骑自行车出行时所行路程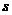 (
( )与时间
)与时间 (
( )的函数关系图象,从中得到的正确信息是( )
)的函数关系图象,从中得到的正确信息是( )
A.整个行程的平均速度为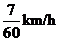 B.前二十分钟的速度比后半小时的速度慢
B.前二十分钟的速度比后半小时的速度慢
C.前二十分钟的速度比后半小时的速度快 D.从起点到达终点,该同学共用了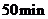
6.若 ,则下列函数①
,则下列函数①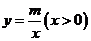 ,②
,② ,③
,③ ,④
,④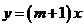 中,
中,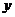 的值随
的值随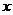 的值增大而增大的函数共有( )函数的性质
的值增大而增大的函数共有( )函数的性质
A. 个 B.
个 B.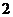 个 C.
个 C. 个 D.
个 D.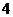 个
个
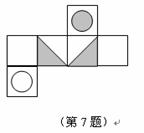
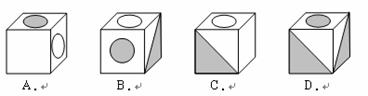
7.如图是某一立方体的侧面展开图,则该立方体是( )
8.下列图形:
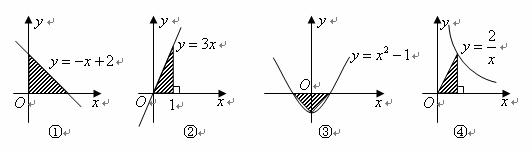
其中,阴影部分的面积相等的是( )函数的性质
A.①② B.②③ C.③④ D.④①
9.如果在正八边形硬纸板上剪下一个三角形(如图①中的阴影部分),那么图②,图③,图④中的阴影部分,均可由这个三角形通过一次平移、对称或旋转而得到.要得到图②,图③,图④中的阴影部分,依次进行的变换不可行的是( )图形变换
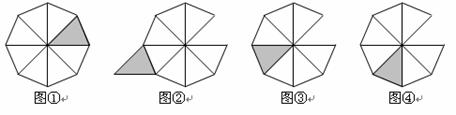
A.平移、对称、旋转 B.平移、旋转、对称
C.平移、旋转、旋转 D.旋转、对称、旋转
10.观察由等腰梯形组成的下图和所给表中数据的规律后回答问题:

当等腰梯形个数为2006时,图形的周长为( )探索规律
A.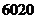 B.
B. C.
C. D.
D.
11.用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素 含量及购买这两种原料的价格如下表:
含量及购买这两种原料的价格如下表:

现配制这种饮料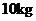 ,要求至少含有
,要求至少含有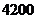 单位的维生素
单位的维生素 ,若所需甲种原料的质量为
,若所需甲种原料的质量为 ,则
,则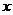 应满足的不等式为( )不等式
应满足的不等式为( )不等式
A. B.
B.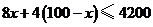
C.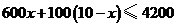 D.
D.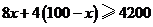
12.如图,在梯形 中,
中,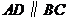 ,
, ,
,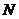 分别是
分别是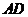 ,
,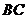 的中点,若
的中点,若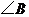 与
与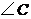 互余,则
互余,则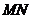 与
与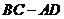 的关系是( )梯形
的关系是( )梯形

A.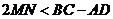 B.
B.
C.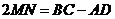 D.
D.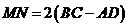
第Ⅱ卷
二、填空题(本大题共7小题,满分21分.只要求填写最后结果,每小题填对得3分)
13.已知点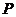 在第四象限,它的横坐标与纵坐标的和为
在第四象限,它的横坐标与纵坐标的和为 ,则点
,则点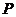 的坐标是_________(写出符合条件的一个点即可).
的坐标是_________(写出符合条件的一个点即可).
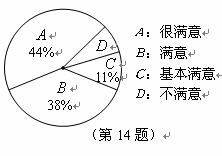
14.某商场为了解本商场服务质量,随机调查了来本商场的 名顾客,调查的结果如图所示,根据图中给出的信息,这
名顾客,调查的结果如图所示,根据图中给出的信息,这 名顾客中对该商场的服务质量表示不满意的有_________名.
名顾客中对该商场的服务质量表示不满意的有_________名.
15.三个袋中各装有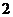 个球,其中第一个袋和第二个袋中各有一个红球和一个黄球,第三个袋中有一个黄球和一个黑球,现从三个袋中各摸出一个球,则摸出的三个球中有
个球,其中第一个袋和第二个袋中各有一个红球和一个黄球,第三个袋中有一个黄球和一个黑球,现从三个袋中各摸出一个球,则摸出的三个球中有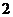 个黄球和一个红球的概率为_________
个黄球和一个红球的概率为_________
16.如图,大楼高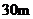 ,远处有一塔
,远处有一塔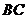 ,某人在楼底
,某人在楼底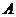 处测得塔顶的仰角为
处测得塔顶的仰角为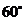 ,爬到楼顶
,爬到楼顶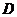 测得塔顶的仰角为
测得塔顶的仰角为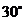 .则塔高
.则塔高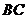 为_________
为_________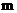 .
.
17.已知等腰三角形一条腰上的高与腰之比为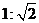 ,那么这个等腰三角形的顶角等于_________.
,那么这个等腰三角形的顶角等于_________.
18.抛物线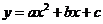 上部分点的横坐标
上部分点的横坐标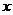 ,纵坐标
,纵坐标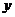 的对应值如下表:二次函数
的对应值如下表:二次函数
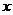
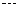

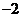
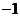


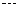
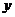
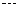
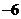

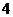
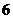
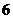
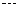
容易看出, 是它与
是它与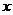 轴的一个交点,则它与
轴的一个交点,则它与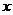 轴的另一个交点的坐标为_________.
轴的另一个交点的坐标为_________.
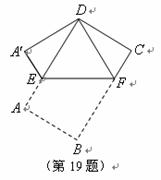
19.将矩形纸片 如图那样折叠,使顶点
如图那样折叠,使顶点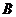 与顶点
与顶点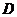 重合,折痕为
重合,折痕为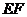 .若
.若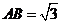 ,
,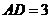 ,则
,则 的周长为_________.矩形
的周长为_________.矩形
三、解答题(本大题共7小题,满分63分.解答应写出必要的文字说明、证明过程或推演步骤)
20.(本小题满分11分)
(1)解不等式组: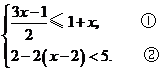 不等式
不等式
(2)化简: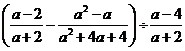 .分式
.分式
21.(本小题满分6分)统计
为了让学生了解环保知识,增强环保意识.某中学举办了一次“环保知识竞赛”活动,共有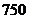 名学生参加了竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计,其中成绩在60.5~70.5分范围内的频率是
名学生参加了竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计,其中成绩在60.5~70.5分范围内的频率是 .请你根据下面尚未完成的频数分布表,解答下列问题:
.请你根据下面尚未完成的频数分布表,解答下列问题:
(1)补全频数分布表;
(2)成绩的中位数落在哪一组内?
(3)若成绩在80分以上(不含80分)为优秀,则该校成绩优秀的学生约为多少人?
频数分布表
分组编号
成绩/分
频数
1
60.5~70.5
6
2
70.5~80.5
12
3
80.5~90.5
18
4
90.5~100.5
合计
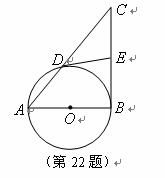
22.(本小题满分8分)圆
已知:如图,以 的边
的边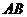 为直径的
为直径的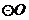 交边
交边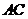 于点
于点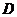 ,且过点
,且过点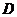 的切线
的切线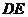 平分边
平分边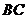 .
.
(1)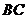 与
与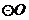 是否相切?请说明理由;
是否相切?请说明理由;
(2)当 满足什么条件时,以点
满足什么条件时,以点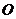 ,
,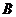 ,
,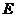 ,
,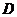 为顶点的四边形是平行四边形?并说明理由.
为顶点的四边形是平行四边形?并说明理由.
23.(本小题满分8分)分式方程
某商场销售某种商品,第一个月将此商品的进价提高 作为销售价,共获利
作为销售价,共获利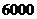 元.第二个月商场搞促销活动,将商品的进价提高
元.第二个月商场搞促销活动,将商品的进价提高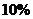 作为销售价,第二个月的销售量比第一个月增加了
作为销售价,第二个月的销售量比第一个月增加了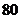 件,并且商场第二个月比第一个月多获利
件,并且商场第二个月比第一个月多获利 元.问此商品的进价是多少元?商场第二个月共销售多少件?
元.问此商品的进价是多少元?商场第二个月共销售多少件?
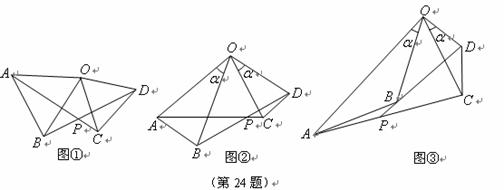
24.(本小题满分10分)三角形
(1)已知:如图①,在 和
和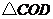 中,
中,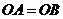 ,
,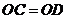 ,
,
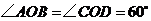 ,求证:①
,求证:①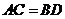 ;②
;②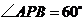 .
.
(2)如图②,在 和
和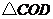 中,若
中,若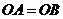 ,
, ,
, ,则
,则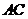 与
与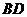 间的等量关系式为________________;
间的等量关系式为________________; 的大小为__________________.
的大小为__________________.
(3)如图③,在 和
和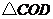 中,若
中,若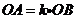 ,
,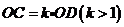 ,
,
 ,则
,则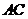 与
与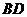 间的等量关系式为_______;
间的等量关系式为_______; 的大小为________.
的大小为________.
25.(本小题满分10分)一次函数与二次函数
如图,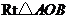 是一张放在平面直角坐标系中的直角三角形纸片,点
是一张放在平面直角坐标系中的直角三角形纸片,点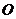 与原点重合,点
与原点重合,点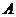 在
在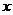 轴上,点
轴上,点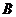 在
在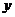 轴上,
轴上, ,
,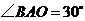 .将
.将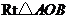 折叠,使
折叠,使 边落在
边落在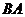 边上,点
边上,点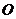 与点
与点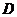 重合,折痕为
重合,折痕为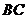 .
.
(1)求直线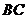 的解析式;
的解析式;
(2)求经过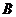 ,
, ,
,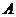 三点的抛物线
三点的抛物线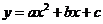 的解析式;若抛物线的顶点为
的解析式;若抛物线的顶点为 ,试判断点
,试判断点 是否在直线
是否在直线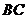 上,并说明理由.
上,并说明理由.

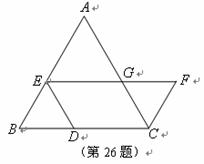
26.(本小题满分10分)梯形
如图,点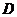 ,
,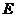 分别在
分别在 的边
的边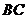 ,
,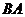 上,四边形
上,四边形 是等腰梯形,
是等腰梯形,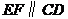 .
.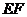 与
与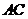 交于点
交于点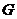 ,且
,且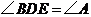 .
.
(1)试问: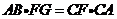 成立吗?说明理由;
成立吗?说明理由;
(2)若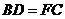 ,求证:
,求证: 是等腰三角形.
是等腰三角形.