高三第2次月考试卷
高三数学试题
满分150分 时间:120分钟 命题人:杨玉姣
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如果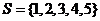 ,
,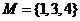 ,
,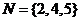 ,那么(
,那么( sM)∩(
sM)∩( sN)等于
sN)等于
A.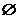 B.
B.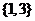 C.
C.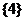 D.
D.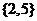
2.若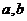 是常数,
则“
是常数,
则“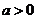 且
且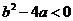 ”是“对任意
”是“对任意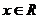 ,有
,有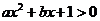 ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3. 下列函数中,在其定义域上是增函数的有
①
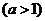 ②
②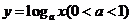
③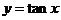 ,
④
,
④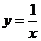 ⑤
⑤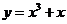
A.1个 B.2个 C .3个 D.4个
4.若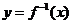 为函数
为函数 的反函数,且
的反函数,且 的图象过点(3,1),则
的图象过点(3,1),则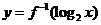 的图象必过点
的图象必过点
A.(1,8) B.(8,1) C.(2,3) D.(3,2)
5.已知函数f(x)=log2(x2-2ax+4-
A. (-∞,-4)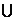 (1,∞) B. [-4,1] C. (-∞,-4]
(1,∞) B. [-4,1] C. (-∞,-4] [1,∞) D. (-4,1)
[1,∞) D. (-4,1)
6.在等比数列 中,若
中,若 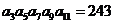 ,则
,则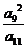 的值为
的值为
A.9
B.
7.设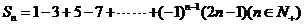 则
则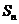 等于
等于
A.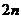 B.
B.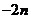 C
C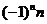 D.
D.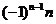
8.函数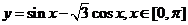 的值域是
的值域是
A.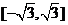 B.
B.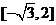 C.
C.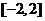 D.
D.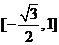
9.椭圆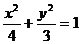 的右焦点到直线
的右焦点到直线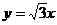 的距离是
的距离是
A.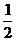 B.
B.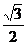 C.1
D.
C.1
D.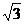
10.(文)设函数f(x)=1-x2+log(x-1),则下列说法正确的是
A.f(x)是增函数,没有最大值,有最小值 B.f(x)是增函数,没有最大值、最小值
C.f(x)是减函数,有最大值,没有最小值 D.f(x)是减函数,没有最大值、最小值
(理)定义在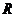 上的奇函数
上的奇函数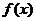 满足
满足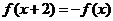 ,且当
,且当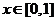 时,
时,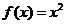 ,则不等式
,则不等式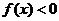 的解集为
的解集为
A.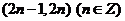 B.
B.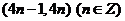
C.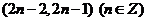 D.
D.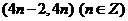
11.为迎接2008年北京奥运会,某校举行奥运知识竞赛,有6支代表队参赛,每队2名同学。若12名参赛同学中有4人获奖,且这4人来自3个不同的代表队,则不同获奖情况种数共有
A.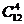 B.
B.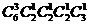
C.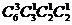 D.
D.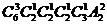
12. 向量 a=(3,4), b=(sinα,cosα), 且a ∥ b, 则tanα=( )
A.
3/4
B. ? 3/
二、填空题:本大题4个小题,每小题5分,共20分,只填结果,不要过程
13.函数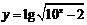 的定义域是 .
的定义域是 .
14.设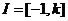 ,若
,若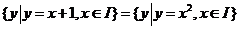 ,则
,则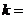
15.函数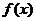 对任意实数
对任意实数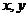 都满足:
都满足: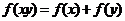 且
且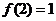 ,则
,则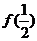 的值是
的值是
16.(文)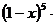 的展开式中
的展开式中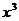 的系数为 .
的系数为 .
(理)化简: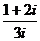 =
.
=
.
高三第2次月考试卷
高三数学试题卡
1
2
3
4
5
6
7
8
9
10
11
12
二、填空题
13. 14. 15. 16.
三、解答题:本大题5个小题,共70分.解答必需写出必要的文字说明、推理过程或计算步骤.
17.已知函数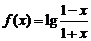 .(1)求
.(1)求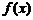 的定义域;(2)求该函数的反函数
的定义域;(2)求该函数的反函数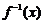 ;
;
(3)判断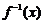 的奇偶性. (本题满分12分)
的奇偶性. (本题满分12分)
18.设等差数列 的前
的前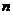 项和为
项和为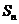 ,且
,且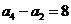 ,
,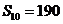 .
.
(1)求数列 的通项公式
的通项公式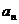 ;
;
(2)设 ,试判断
,试判断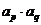 是否仍为数列
是否仍为数列 中的项,并说明理由.(本题10分)
中的项,并说明理由.(本题10分)
19.(本题满分10分)
|
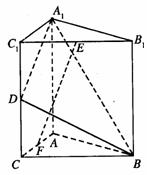
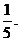
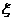 表示所选用的两种不同添加剂的芳香度之和。
表示所选用的两种不同添加剂的芳香度之和。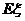 ,(要求写出计算过程或说明道理)
,(要求写出计算过程或说明道理)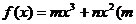 、
、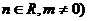 ,函数
,函数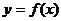 的图象在点(2,f(2))处的切线与x轴平行.
的图象在点(2,f(2))处的切线与x轴平行.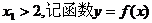 的图象在点M
的图象在点M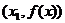 处的切线为
处的切线为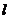 ,设
,设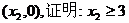 .(本题满分14分)
.(本题满分14分) 15、-1
15、-1
 ……9分
……9分 ………………10分
………………10分
 设平面A1BD的法向量为n
设平面A1BD的法向量为n

 …………8分
…………8分 …………9分
…………9分 ………………10分
………………10分
 ………………6分
………………6分 ……………………12分
……………………12分




 (y-1)代入3x2-y2=1有(3-k2)y2-6y+3-k2=0,显然k2=3时,直线与双曲线渐近线平行,无二公共点,所以k2≠3.由y∈R,所以Δ=36-4(3-k2)2≥0,所以0<k2<6,且k2≠3.综合知k≠(-
(y-1)代入3x2-y2=1有(3-k2)y2-6y+3-k2=0,显然k2=3时,直线与双曲线渐近线平行,无二公共点,所以k2≠3.由y∈R,所以Δ=36-4(3-k2)2≥0,所以0<k2<6,且k2≠3.综合知k≠(- ,
, )且k≠±
)且k≠± 时,直线与双曲线交于二点,反之亦然.
时,直线与双曲线交于二点,反之亦然. ,x1x2=
,x1x2= ,由(1)知y1y2=1,因为圆过原点,以AB为直径,所以x1x2+y1y2=0,所以k2=1,即k=±1为所求的值.
,由(1)知y1y2=1,因为圆过原点,以AB为直径,所以x1x2+y1y2=0,所以k2=1,即k=±1为所求的值.
 ………………2分
………………2分
 ………………4分
………………4分 ………………5分
………………5分 ………………6分
………………6分
 ………………7分
………………7分 的单调递增区间为
的单调递增区间为
 时,函数
时,函数

 …………10分
…………10分 ………………11分
………………11分
 ……………………14分
……………………14分