2007年福建省泉州市初中毕业、升学考试
数 学 试 题
(满分:150分;考试时间:120分钟)
一、选择题(每小题4分,共24分)每题有四个答案,其中有且只有一个答案是正确的,请在答题卡相应题目的答题区域内作答,答对的得4分,答错、不答或答案超过一个的一律得0分。
1.计算2-3=( )
A.-1 B.
2.甲、乙两同学近期5次百米跑测试成绩的平均数相同,甲同学成绩的方差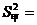 4,乙同学成绩的方差
4,乙同学成绩的方差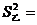 3.1,则对他们测试成绩的稳定性判断正确的是( )
3.1,则对他们测试成绩的稳定性判断正确的是( )
A.甲的成绩较稳定 B.乙的成绩较稳定
C.甲、乙成绩的稳定性相同 D.甲、乙成绩的稳定性无法比较
3.观察下列图形,其中不是正方体的展开图的为( )
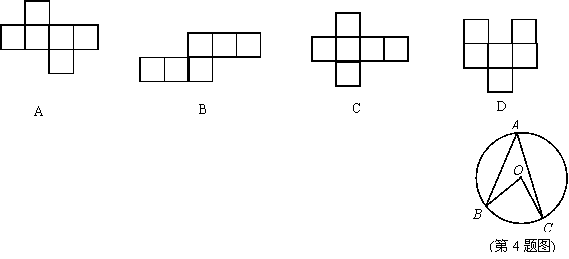
4.如图,A、B、C三点都在⊙O上,若∠BOC=80°,则∠A的度数等于( )
A.20° B.40° C.60° D.80°
5.不等式组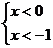 的解集的情况为( )
的解集的情况为( )
A.x<-1
B.x<
6.将点A(4,0)绕着原点O顺时针方向旋转30°角到对应点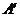 ,则点
,则点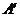 的坐标是( )
的坐标是( )
A.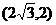 B.(4,-2)
C.
B.(4,-2)
C.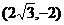 D.
D.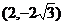
二、填空题(每小题3分,共36分)在答题卡上相应题目的答题区域内作答。
7.计算: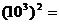
8.分解因式: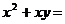
9.据泉州统计信息网公布的数据显示,2006年泉州市全年旅游总收入约为14 600 000 000,用科学记数法表示约为 元
10.一种商品原价120元,按八折(即原价的80%)出售,则现售价应为 元
11.某水果店1至6月份的销售情况(单位:千克)为450、440、420、480、580、550,则这组数据的极差是 千克
 12.计算:
12.计算: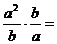
13.五边形的内角和等于 度
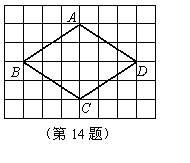
14.在右图的方格纸中有一个菱形ABCD(A、B、C、D四点均为格点),
若方格纸中每个最小正方形的边长为1,则该菱形的面积为
15.反比例函数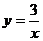 的图象在第一象限与第 象限
的图象在第一象限与第 象限
16.已知圆锥的底面半径为10,侧面积是300π,则这个圆锥的母线长为
17.口袋中放有黄、白、红三种颜色的小球各1个,这3个球除颜色外没有任何区别,随机从口袋中任取1个球,写出这个实验中一个可能发生的事件:
 18.图(1)是一个黑色的正三角形,顺次连结它的三边的中点,得到如图(2)所示的第2个图形(它的中间为一个白色的正三角形);在图(2)的每个黑色的正三角形中分别重复上述的作法,得到如图(3)所示的第3个图形。如此继续作下去,则在得到的第6个图形中,白色的正三角形的个数是
18.图(1)是一个黑色的正三角形,顺次连结它的三边的中点,得到如图(2)所示的第2个图形(它的中间为一个白色的正三角形);在图(2)的每个黑色的正三角形中分别重复上述的作法,得到如图(3)所示的第3个图形。如此继续作下去,则在得到的第6个图形中,白色的正三角形的个数是
……
三、解答题(共90分)在答题卡上相应题目的答题区域内作答。
19.(8分)计算:

20.(8分)先化简下面的代数式,再求值:
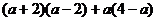 ,其中
,其中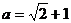
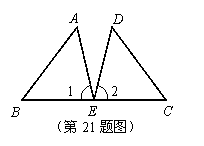 21.(8分)如图,E是BC的中点,∠1=∠2,AE=DE。
21.(8分)如图,E是BC的中点,∠1=∠2,AE=DE。
求证:AB=DC
22.(8分)在“心系灾区”自愿捐款活动中,某班30名同学的捐款情况如下表:
捐款(元)
5
10
15
20
25
30
人数
11
9
6
2
1
1
⑴问这个班级捐款总数是多少元?
⑵求这30名同学捐款的平均数。
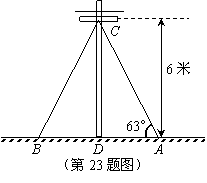 23.(8分)如图,在电线杆里地面
23.(8分)如图,在电线杆里地面
和地面成63°角,求缆绳AC的长(精确到
24.(8分)初三年(1)班要举行一场毕业联欢会,规定每个同学同时转动下图中①、②两个转盘(每个转盘分别被二等分和三等分),若两个转盘停止后指针所指的数字之和为奇数,则这个同学要表演唱歌节目;若数字之和为偶数,则要表演其他节目。试求出这个同学表演唱歌节目的概率(要求用树状图或列表方法求解)
 |
25.(8分)如图,在梯形ABCD中,AD∥BC,∠B=∠ACD
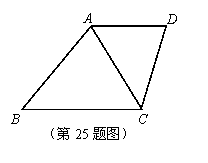 ⑴请再写出图中另外一对相等的角;
⑴请再写出图中另外一对相等的角;
⑵若AC=6,BC=9,试求梯形ABCD的中位线的长度。
26.(8分)已知正n边形的周长为60,边长为a
⑴当n=3时,请直接写出a的值;
⑵把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b。有人分别取n等于3、20、120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等。”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值。
27.(13分)李明从泉州乘汽车沿高速公路前往A地,已知该汽车的平均速度是100千米/小时,它行驶t小时后距泉州的路程为s
⑴请用含t的代数式表示s1;
⑵设另有王红同时从A地乘汽车沿同一条高速公路回泉州,已知这辆汽车距泉州的路程s2(千米)与行驶时间t(时)之间的函数关系式为s2=kt+b(k、t为常数,k≠0),若李红从A地回到泉州用了9小时,且当t=2时,s2=560.
①求k与b的值;
②试问在两辆汽车相遇之前,当行驶时间t的取值在什么范围内,两车的距离小于
28.(13分)已知抛物线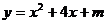 (m为常数)经过点(0,4)
(m为常数)经过点(0,4)
⑴求m的值;
⑵将该抛物线先向右、再向下平移得到另一条抛物线。已知这条平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为l1)关于y轴对称;它所对应的函数的最小值为-8.
①试求平移后的抛物线所对应的函数关系式;
②试问在平移后的抛物线上是否存在着点P,使得以3为半径的⊙P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被⊙P所截得的弦AB的长度;若不存在,请说明理由。
四、附加题:(共10分)在答题卡上相应题目的答题区域内作答。
友情提示:请同学们做完上面考题后,再认真检查一遍,估计一下你的得分情况,如果你全卷得分低于90分(及格线),则本题的得分将计入全卷得分,但计入后全卷总分最多不超过90分;如果你全卷总分已经达到或超过90分,则本题的得分不计入总分。
 1.(5分)填空:(-2)×(-3)=
1.(5分)填空:(-2)×(-3)=
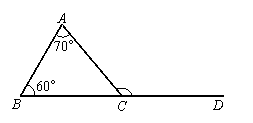
2.(5分)填空:如图:在△ABC中,∠A=70°,∠B=60°,
点D在BC的延长线上,则∠ACD= 度.