绝密★启用前 试卷类型:A
山东省二○○七年中等学校招生考试(课标卷)
数 学 试 题
注意事项:
1. 本试题分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷4页为选择题,36分;第Ⅱ卷8页为非选择题,84分;全卷共12页,满分120分,考试时间为120分钟.
2. 答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上,考试结束,试题和答题卡一并收回.
3. 第Ⅰ卷每题选出答案后,必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑.如需改动,先用橡皮擦干净,再改涂其它答案.
第Ⅰ卷(选择题 共36分)
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1.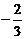 的绝对值是
的绝对值是
(A)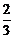 (B)
(B)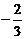
(C)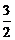 (D)
(D)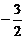
2.下列事件中,是必然事件的是
(A)购买一张彩票中奖一百万元
(B)打开电视机,任选一个频道,正在播新闻
(C)在地球上,上抛出去的篮球会下落
(D)掷两枚质地均匀的正方体骰子,点数之和一定大于6
3.下列算式中,正确的是
(A)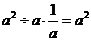
(B)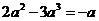
(C)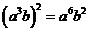
(D)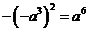
4.如图1放置的一个机器零件,若其主视图如图2,则其俯视图是
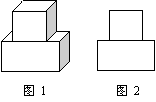
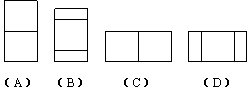
5.不等式2x-7<5-2x的正整数解有
(A)1个
(B)2个
(C)3个
(D)4个
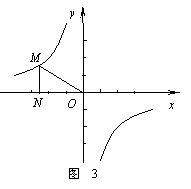 6.反比例函数
6.反比例函数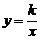 的图象如图3所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果
的图象如图3所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果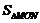 =2,
=2,
则k的值为
(A)2
(B)-2
(C)4
(D)-4
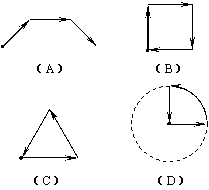
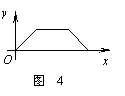
7.图4是韩老师早晨出门散步时,离家的距离(y)与时间(x)之间的函数图象.若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是
 |
|||
 |
|||
8.若方程组
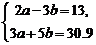 的解是
的解是 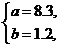 则方程组
则方程组
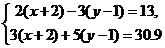
的解是
(A)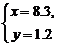 (B)
(B)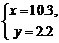
(C)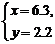 (D)
(D)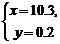
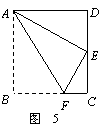
9.如图5,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于
 (A)
(A)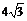
(B)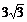
(C)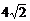
(D)8
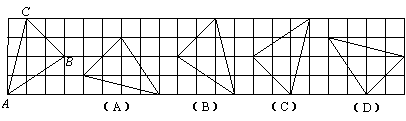 10. 在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是
10. 在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是
11.一个圆锥的高为3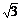 ,侧面展开图是半圆,则圆锥的侧面积是
,侧面展开图是半圆,则圆锥的侧面积是
(A)9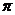 (B)18
(B)18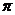
(C)27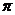 (D)39
(D)39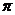
12.王英同学从A地沿北偏西60º方向走
(A)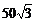 m
m
(C) m
m
绝密★启用前 试卷类型:A
山东省二○○七年中等学校招生考试(课标卷)
数 学 试 题
第Ⅱ卷(非选择题 共84分)
注意事项:
1.第Ⅱ卷共8页,用钢笔或圆珠笔直接写在试卷上.
2.答卷前将密封线内的项目填写清楚.
题号
二
三
总分
18
19
20
21
22
23
24
得分
二、填空题:本大题共5小题,共20分,只要求填写最后结果,每小题填对得4分.
 13. 2007年4月,全国铁路进行了第六次大提速,提速后的线路时速达200千米.共改造约6000千米的提速线路,总投资约296亿元人民币,那么,平均每千米提速线路的投资约 亿元人民币(用科学记数法,保留两个有效数字).
13. 2007年4月,全国铁路进行了第六次大提速,提速后的线路时速达200千米.共改造约6000千米的提速线路,总投资约296亿元人民币,那么,平均每千米提速线路的投资约 亿元人民币(用科学记数法,保留两个有效数字).
14.分解因式: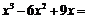 .
.
15.如图6,△ABC内接于⊙O,∠BAC=120°,
AB=AC,BD为⊙O的直径,AD=6,则BC等于
.
 16.从-2,-1,1,2这四个数中,任取两个不同的数作为一次函数
16.从-2,-1,1,2这四个数中,任取两个不同的数作为一次函数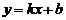 的系数
的系数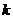 ,
,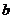 ,则一次函数
,则一次函数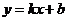 的图象不经过第四象限的概率是________.
的图象不经过第四象限的概率是________.
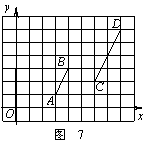
17.线段AB,CD在平面直角坐标系中的
位置如图7所示,O为坐标原点.若线段AB
上一点P的坐标为(a,b),则直线OP与线段
CD的交点的坐标为 .
三、解答题:本大题共7小题,共64分.解答要写出必要的文字说明、证明过程或演算步骤.
18. (本题满分6分)
解方程: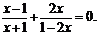
19. (本题满分9分)
将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率如下表(未完成):
数据段
频 数
频 率
30~40
10
0.05
40~50
36
50~60
0.39
60~70
70~80
20
0.10
总 计
1
注:30~40为时速大于等于
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
 (3)如果此地汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
(3)如果此地汽车时速不低于60千米即为违章,则违章车辆共有多少辆?

20.(本题满分9分)
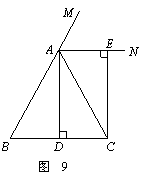 已知:如图9,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
已知:如图9,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形
ADCE是一个正方形?并给出证明.
21. (本题满分10分)
某公司专销产品A,第一批产品A上市40天内全部售完.该公司对第一批产品A上市后的市场销售情况进行了跟踪调查,调查结果如图所示,其中图10中的折线表示的是市场日销售量与上市时间的关系;图11中的折线表示的是每件产品A的销售利润与上市时间的关系.
(1)试写出第一批产品A的市场日销售量y与上市时间t的关系式;
 (2)第一批产品A上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?
(2)第一批产品A上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?

22. (本题满分10分)
在平面直角坐标系中,△AOB的位置如图12所示,已知∠AOB=90º,AO=BO,点A的坐标为(-3,1).
(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)设点B关于抛物线的对称轴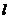 的对称点为B1,求△AB1B的面积.
的对称点为B1,求△AB1B的面积.
 |


23. (本题满分10分)
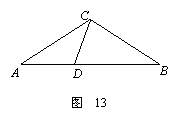
已知:如图13,在△ABC中,D为AB边上一点,∠A=36º,AC=BC,
AC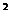 =AB?AD.
=AB?AD.
(1)试说明:△ADC和△BDC都是等腰三角形;
(2)若AB=1,求AC的值;
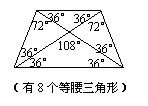
(3)试构造一个等腰梯形,该梯形连同它的两条对角线,得到了8个三角形,要求构造出的图形中有尽可能多的等腰三角形.(标明各角的度数)
 |
24. (本题满分10分)
根据以下10个乘积,回答问题:
11×29; 12×28; 13×27; 14×26; 15×25;
16×24; 17×23; 18×22; 19×21; 20×20.
(1)试将以上各乘积分别写成一个“□2-○
(2)将以上10个乘积按照从小到大的顺序排列起来;
(3)试由⑴、⑵猜测一个一般性的结论.(不要求证明)
评卷说明:
1.选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分.
2.解答题每小题的解答中所对应的分数,是指考生正确解答到该步骤所应得的累计分数.本答案对每小题只给出一种或两种解法,对考生的其他解法,请参照评分意见进行评分.
3.如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确解答分数的一半;若出现严重的逻辑错误,后续部分就不再给分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
C
D
B
D
D
C
A
B
B
D
二、填空题 (本大题共5小题,每小题4分,共20分) :
13.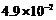 ;14.
;14.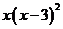 ;15.6;16.
;15.6;16.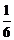 ;17.(
;17.(
三、解答题 (本大题共7小题,共64分) :
18.(本题满分6分)
解:两边同乘以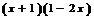 ,
,
得 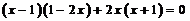 ; ……………………………3分
; ……………………………3分
整理,得 5x-1=0;
解得 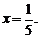 ……………………………………………5分
……………………………………………5分
经检验,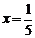 是原方程的根. ……………………………………6分
是原方程的根. ……………………………………6分
19.(本题满分9分)
解:(1)如表:
数据段
频 数
频 率
30~40
10
0.05
40~50
36
0.18
50~60
78
0.39
60~70
56
0.28
70~80
20
0.10
总 计
200
1
…………………………………………………………………………3分
(2)如图:
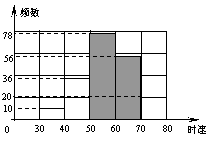
………………8分
|
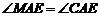 .
.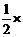 180°=90°.……………4分
180°=90°.……………4分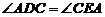 =90°,
=90°,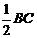 时,四边形ADCE是正方形.…………6分
时,四边形ADCE是正方形.…………6分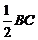 ,
,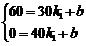
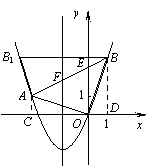 则∠ACO=∠ODB=90º,
则∠ACO=∠ODB=90º,  .
.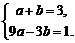 解得
解得 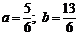 . ……………………6分
. ……………………6分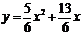 . …………………7分
. …………………7分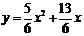 中,对称轴l的方程是
中,对称轴l的方程是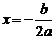 =
=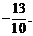 …………………………………8分
…………………………………8分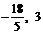 ).
…………………………………9分
).
…………………………………9分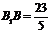 ,高的长为2.
,高的长为2.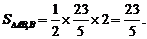 ……………………………………10分
……………………………………10分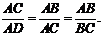
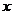 ,则
,则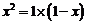 ,即
,即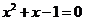 . …………6分
. …………6分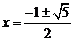 ,∴
,∴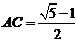 (负根舍去). …………7分
(负根舍去). …………7分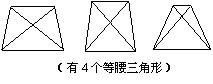 (3)说明:按照画出的梯形中,有4个,6个和8个等腰三角形三种情况分别给分.
(3)说明:按照画出的梯形中,有4个,6个和8个等腰三角形三种情况分别给分. 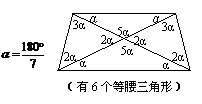
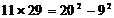 . …………………6分
. …………………6分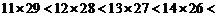
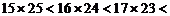
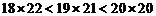 .
…………………………7分
.
…………………………7分 ,a,b是自然数,则ab≤202=400. ………8分
,a,b是自然数,则ab≤202=400. ………8分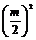 . ……………9分
. ……………9分