2009届山东英雄山中学 高三年级期末测试
高三年级期末测试
数学试题(理科)
一、选择题:本大题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如果直线 等于 ( )
等于 ( )
A.―3 B.― D.
D.
2.已知命题 下列结论中正确的是 ( )
下列结论中正确的是 ( )
A.命题“ ”是真命题 B.命题“
”是真命题 B.命题“ ”是真命题
”是真命题
C.命题“ ”是真命题 D.命题“
”是真命题 D.命题“ ”是假命题
”是假命题
3.已知 的值为 ( )
的值为 ( )
A. B.
B. C.
C. D.
D.
4.函数 处的切线方程为 ( )
处的切线方程为 ( )
A. B.
B. C.
C. D.
D.
|




 则下列不等式成立的是 ( )
则下列不等式成立的是 ( ) B.
B.
 D.
D.



 的交点中,距离最近的两点间的距离为
的交点中,距离最近的两点间的距离为 ,那么此函数的最小正周期是 ( )
,那么此函数的最小正周期是 ( )



 D.
D.

 B.
B.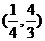
 D.
D.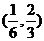
 的终边所在直线方程为
。
的终边所在直线方程为
。 则△AOB与△AOC面积之比是 。
则△AOB与△AOC面积之比是 。 ,且在[―1,0]上是增函数,给出下面关于
,且在[―1,0]上是增函数,给出下面关于 :①
:① 是周期函数;②
是周期函数;② 对称;③
对称;③ 其中正确的命题序号是 。(注:把你认为正确的命题序号都填上)
其中正确的命题序号是 。(注:把你认为正确的命题序号都填上) ;
; ;
; ;
; ;
; ;
;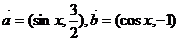
 的值;
的值; 上的值域。
上的值域。 和定义A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点Q,且满足|PQ|=|PA|。
和定义A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点Q,且满足|PQ|=|PA|。
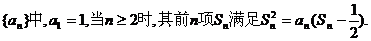
 ;
; ;
; 成立?若存在,求出m的最大值;若不存在,请说明理由。
成立?若存在,求出m的最大值;若不存在,请说明理由。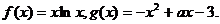
 上的最小值;
上的最小值; 的取值范围;
的取值范围; 成立.
成立. 14.1:2 15.①②⑤ 16.⑤
14.1:2 15.①②⑤ 16.⑤ 共线
共线
 ………………3分
………………3分 …………6分
…………6分

 …………12分
…………12分
 ,
, .
.

 .……9分
.……9分 .
.
 OQ,
OQ,


 …………3分
…………3分
 …………6分
…………6分 时,
时, 线段PQ长取最小值
线段PQ长取最小值 …………7分
…………7分 即R
即R 且R
且R

 ,此时b=―
,此时b=―
 …………12分
…………12分

 平面BCD1,BO
平面BCD1,BO 平面BCD1
平面BCD1

 …………12分
…………12分



 上是增函数
上是增函数


 单调递增。 …………2分
单调递增。 …………2分 ,不等式无解;
,不等式无解; ;
; ;
; …………5分
…………5分 , …………6分
, …………6分
 ……10分
……10分 ,
,


 成立。
成立。