日照实验高中2004级模块考试(必修2)
一、选择题
1. 已知直线经过点A(0,4)和点B(1,2),则直线AB的斜率为( B )
A.3
B.
2.过点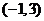 且平行于直线
且平行于直线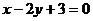 的直线方程为( A )
的直线方程为( A )
A.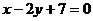 B.
B.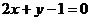 C.
C.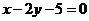 D.
D.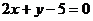
3. 下列说法不正确的是( D )
A. 空间中,一组对边平行且相等的四边形是一定是平行四边形;
B.同一平面的两条垂线一定共面;
C. 过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内;
D. 过一条直线有且只有一个平面与已知平面垂直.
4.已知点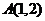 、
、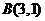 ,则线段
,则线段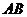 的垂直平分线的方程是( B )
的垂直平分线的方程是( B )
A.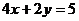 B.
B.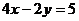 C.
C.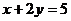 D.
D.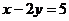
5. 在同一直角坐标系中,表示直线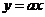 与
与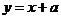 正确的是( C )
正确的是( C )
 A. B. C. D.
A. B. C. D.
6. 已知a、b是两条异面直线,c∥a,那么c与b的位置关系( C )
A.一定是异面 B.一定是相交 C.不可能平行 D.不可能相交
7. 设m、n是两条不同的直线,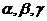 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若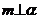 ,
,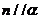 ,则
,则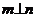 ②若
②若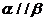 ,
,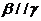 ,
,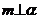 ,则
,则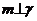
③若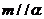 ,
,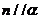 ,则
,则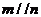 ④若
④若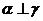 ,
,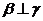 ,则
,则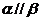
其中正确命题的序号是 ( A )
(A)①和② (B)②和③ (C)③和④ (D)①和④
8. 圆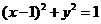 与直线
与直线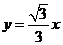 的位置关系是( A )
的位置关系是( A )
A.相交 B. 相切 C.相离 D.直线过圆心
9. 两圆相交于点A(1,3)、B(m,-1),两圆的圆心均在直线x-y+c=0上,则m+c的值为( A )
A.-1 B.
10. 在空间四边形ABCD各边AB、BC、CD、DA上分别取E、F、G、H四点,如果EF、GH相交于点P,那么( A )
A.点P必在直线AC上 B.点P必在直线BD上
C.点P必在平面DBC内 D.点P必在平面ABC外
11. 若M、N分别是△ABC边AB、AC的中点,MN与过直线BC的平面β的位置关系是(C )
A.MN∥β
B.MN与β相交或MN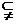 β
β
C. MN∥β或MN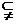 β
D. MN∥β或MN与β相交或MN
β
D. MN∥β或MN与β相交或MN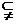 β
β
12. 已知A、B、C、D是空间不共面的四个点,且AB⊥CD,AD⊥BC,则直线BD与AC( A )
A.垂直 B.平行 C.相交 D.位置关系不确定
二 填空题
13.已知A(1,-2,1),B(2,2,2),点P在z轴上,且|PA|=|PB|,则点P的坐标为 ;
14.已知正方形ABCD的边长为1,AP⊥平面ABCD,且AP=2,则PC= ;
15. 过点(1,2)且在两坐标轴上的截距相等的直线的方程 ___________;
16.圆心在直线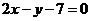 上的圆C与
上的圆C与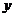 轴交于两点
轴交于两点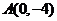 ,
,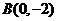 ,则圆C的方程为 .
,则圆C的方程为 .
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
D
B
C
C
A
A
C
A
C
A
二、填空题:(
13. (0,0,3) 14. 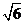 15 y=2x或x+y-3=0 16. (x-2)2+(y+3)2=5
15 y=2x或x+y-3=0 16. (x-2)2+(y+3)2=5
三 解答题
17(12分) 已知△ABC三边所在直线方程为AB:3x+4y+12=0,BC:4x-3y+16=0,CA:2x+y-2=0
求AC边上的高所在的直线方程.
由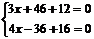 解得交点B(-4,0),
解得交点B(-4,0),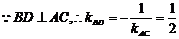 . ∴AC边上的高线BD的方程
. ∴AC边上的高线BD的方程
为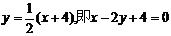 .
.
 18(12分) 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=
18(12分) 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=
 (1) FD∥平面ABC;
(1) FD∥平面ABC;
(2) AF⊥平面EDB.
(1)取AB的中点M,连FM,MC,
∵ F、M分别是BE、BA的中点 ∴ FM∥EA, FM=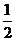 EA
EA
∵ EA、CD都垂直于平面ABC ∴ CD∥EA∴ CD∥FM
又 DC=a, ∴ FM=DC ∴四边形FMCD是平行四边形
∴ FD∥MC
FD∥平面ABC
(2) 因M是AB的中点,△ABC是正三角形,所以CM⊥AB
又 CM⊥AE,所以CM⊥面EAB, CM⊥AF, FD⊥AF,
因F是BE的中点, EA=AB所以AF⊥EB.
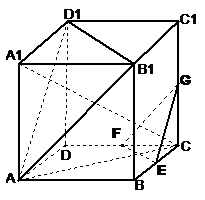 19(12分)如图,在正方体ABCD-A1B
19(12分)如图,在正方体ABCD-A1B
(1) 求证:平面A B1D1∥平面EFG;
(2) 求证:平面AA
20(12分) 已知圆C同时满足下列三个条件:①与y轴相切;②在直线y=x上截得弦长为2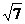 ;③圆心在直线x-3y=0上.
求圆C的方程.
;③圆心在直线x-3y=0上.
求圆C的方程.
设所求的圆C与y轴相切,又与直线交于AB,
∵圆心C在直线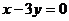 上,∴圆心C(
上,∴圆心C(
与y轴相切,∴R=3|a|. 又圆心C到直线y-x=0的距离
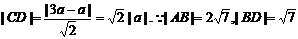
在Rt△CBD中,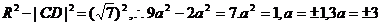 .
.
∴圆心的坐标C分别为(3,1)和(-3,-1),故所求圆的方程为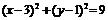
或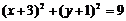 .
.
21(12分) 设有半径为3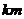 的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
解:如图建立平面直角坐标系,由题意
可设A、B两人速度分别为3v千米/小时 ,
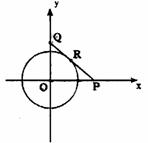 v千米/小时,再设出发x0小时,在点P改变
v千米/小时,再设出发x0小时,在点P改变
方向,又经过y0小时,在点Q处与B相遇.
则P、Q两点坐标为(3vx0, 0),(0,vx0+vy0).
由|OP|2+|OQ|2=|PQ|2知,………………3分
(3vx0)2+(vx0+vy0)2=(3vy0)2,
即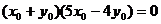 .
.
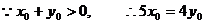 ……①………………6分
……①………………6分
将①代入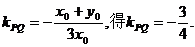 ……………8分
……………8分
又已知PQ与圆O相切,直线PQ在y轴上的截距就是两个相遇的位置.
设直线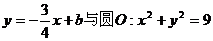 相切,
相切,
则有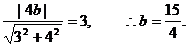 ……………………11分
……………………11分
答:A、B相遇点在离村中心正北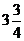 千米处………………12分
千米处………………12分
22(14分)已知圆C: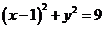 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1) 当l经过圆心C时,求直线l的方程;
(2) 当弦AB被点P平分时,写出直线l的方程;
(3) 当直线l的倾斜角为45º时,求弦AB的长.
(1)
已知圆C: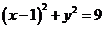 的圆心为C(1,0),因直线过点P、C,所以直线l的斜率为2,
的圆心为C(1,0),因直线过点P、C,所以直线l的斜率为2,
直线l的方程为y=2(x-1),即 2x-y-20.
(2)
当弦AB被点P平分时,l⊥PC,
直线l的方程为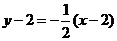 , 即 x+2y-6=0
, 即 x+2y-6=0
(3) 当直线l的倾斜角为45º时,斜率为1,直线l的方程为y-2=x-2 ,即 x-y=0
圆心C到直线l的距离为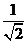 ,圆的半径为3,
,圆的半径为3,
弦AB的长为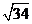 .
.