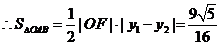江苏省淮阴中学2006年度高二第一学期期中考试试卷
命题:蒋行彪 审校:朱益明
一、选择题(每题5分,共60分)
1.已知函数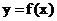 在
在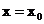 处的导数为
处的导数为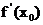 ,若
,若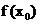 为函数
为函数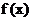 的极大值,则必有
( C
)
的极大值,则必有
( C
)
A.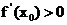 B.
B.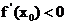 C.
C.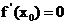 D.
D.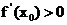 或
或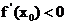
2.关于频率分布直方图,下列有关说法正确的是 ( D )
A.直方图的高表示取某数的频率
B.直方图的高表示该组上的个体在样本中出现的频率
C.直方图的高表示取某组上的个体在样本中出现的频数与组距的比值
D.直方图的高表示取该组上的个体在样本中出现的频率与组距的比值
3.若样本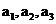 的方差是2,则样本
的方差是2,则样本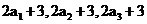 的标准差为( C )
的标准差为( C )
A.2
B. D.8
D.8
4.函数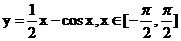 的最大值为
( A
)
的最大值为
( A
)
A.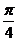 B.
B.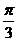 C.
C.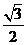 D.2
D.2
5.某班委会由4名男生与3名女生组成,现从中选出2人担任正副班长,至少有1名女生当选的概率为 ( C )
A.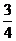 B.
B. C.
C.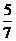 D.
D.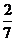
6.双曲线的渐近线方程为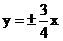 ,则双曲线的离心率为
( D )
,则双曲线的离心率为
( D )
A.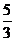 B.
B.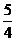 C.
C.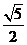 或
或 D.
D.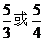
7.在等腰三角形ABC中,过直角顶点C在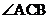 内部任作一条射线CM,与线段AB交于点M,则AM < AC的概率为
( B
)
内部任作一条射线CM,与线段AB交于点M,则AM < AC的概率为
( B
)
A. B.
B.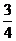 C.
C. D.
D.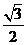
8.过双曲线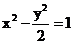 的右焦点F作直线L交双曲线于A、B两点,若|AB| = 4,则这样的直线有
( C
)
的右焦点F作直线L交双曲线于A、B两点,若|AB| = 4,则这样的直线有
( C
)
A.1条 B.2条 C.3条 D.4条
9.国家机关用监听录音机记录了两个间谍的谈话,发现了30 min长的磁带上,从开始30s处起,有10s长的一段内容包含两间谍犯罪的信息,后来发现,这段谈话的一部分被某工作人员擦掉了,该工作人员声称她完全是无意中按错了键,使从此处起往后的所有内容都被擦掉了,那么由于按错了键使含有犯罪内容的谈话被部分或全部擦掉的概率为( D )
A.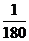 B.
B.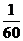 C.
C.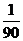 D.
D.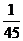
10.椭圆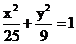 上点P到右焦点距离为3.6,则点P到左准线距离为 ( B
)
上点P到右焦点距离为3.6,则点P到左准线距离为 ( B
)
A.4.5
B.
11.抛物线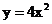 上的一点M到焦点的距离为1,则点M的纵坐标为
( B )
上的一点M到焦点的距离为1,则点M的纵坐标为
( B )
A.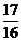 B.
B.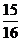 C.
C.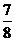 D.0
D.0
12.已知命题P:若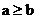 ,则
,则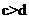 ,命题Q:若
,命题Q:若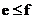 ,则
,则 。若P为真且Q的否命题为真,则“
。若P为真且Q的否命题为真,则“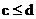 ”是“
”是“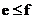 的”
( A
)
的”
( A
)
A.充分条件 B.必要条件 C.充要条件 D.既不充分也不必要条件
二、填空题(每题5分,共30分)
13.已知曲线C: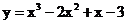 ,则曲线C在点P(2,a)处的切线方程为
,则曲线C在点P(2,a)处的切线方程为
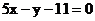
14.函数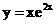 的单调增区间为
的单调增区间为 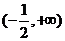
15.已知点A(1,2),F(2,0),点P为椭圆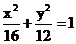 上一点,则 |PA| + 2|PF| 的最小值为 7
上一点,则 |PA| + 2|PF| 的最小值为 7
16.已知命题P:方程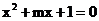 有两个不等的负实根。命题Q:方程
有两个不等的负实根。命题Q:方程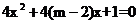 无实根。若“P或Q”为真,“P且Q”为假,则实数m的取值范围是
无实根。若“P或Q”为真,“P且Q”为假,则实数m的取值范围是 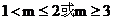
17.已知 为椭圆
为椭圆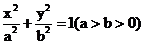 的两个焦点,过
的两个焦点,过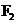 作椭圆的弦AB,若△
作椭圆的弦AB,若△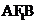 的周长为16,椭圆的离心率为
的周长为16,椭圆的离心率为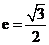 ,则椭圆的方程为
,则椭圆的方程为 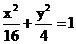
18.已知抛物线
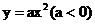 ,焦点为F,过F作直线L交抛物线于A、B两点,则
,焦点为F,过F作直线L交抛物线于A、B两点,则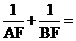 -
-
三、解答题(共70分)
19.(本题满分12分)
已知长、宽分别为16,10的矩形纸板,在其四个角处分别截去相同的小正方形做出一个无盖的盒子,求盒子的最大容积。
解:设小正方形边长为x,则
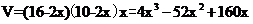
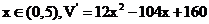
令 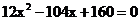 得
得 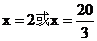
而 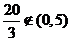
又 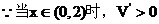
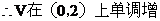
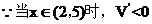
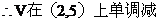
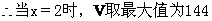
答: 盒子的最大容积为 144 。
20.(本题满分14分)
一次口试,每位考生要在8道口试题中随机抽出2道题回答,若答对其中1题即为及格。(1)现有某位考生会答8道题中的5道题,那么,这位考生及格的概率有多大?
(2)如果一位考生及格的概率小于50%,则他最多只会几道题?
解:(1)8道题中任抽2道题的方法有28种,其中两道题都在不会答的3道题中抽出的方法有3种,故及格的概率为 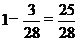 。
。
(2)如果他会3道题,则两题都不会答的方法有10种,及格概率仍 >
50%,当他只会2道题时,抽到2题都不会的方法数为15种。此时他及格的概率为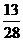 < 50%,即他最多会2题。
< 50%,即他最多会2题。
21.(本题满分14分)
已知两定点A、B距离为6,动点M满足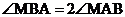 ,求动点M的轨迹方程。
,求动点M的轨迹方程。
解:直线AB为x轴,线段AB的垂直平分线为y轴,建立直角坐标系,
则 A(-3,0),B(3,0),设M(x,y)
则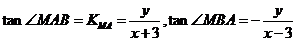
依题意得: 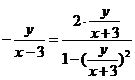 化简得:
化简得:
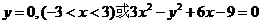
所以动点M的轨迹方程为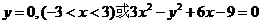
22.(本题满分14分)
一顶点在坐标原点,焦点在x轴上的抛物线截直线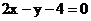 所得的弦长为
所得的弦长为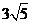 ,求抛物线的方程。
,求抛物线的方程。
解:设抛物线方程为 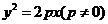
将直线方程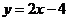 代入抛物线方程,并整理得:
代入抛物线方程,并整理得: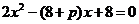
设方程的两个根为 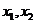 , 则根据韦达定理有
, 则根据韦达定理有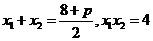
由弦长公式得: 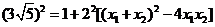
即: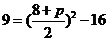
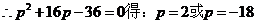
故所求抛物线的方程 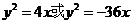
23.(本题满分16分)
椭圆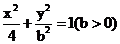 的焦点在x轴上,其右顶点关于直线
的焦点在x轴上,其右顶点关于直线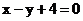 的对称点在椭圆的左准线上。
的对称点在椭圆的左准线上。
(1)求椭圆的方程;
(2)过椭圆左焦点F的直线L交椭圆于A、B两点,交椭圆左准线于C点,设O为坐标原点,且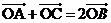 ,求△OAB的面积。
,求△OAB的面积。
解:(1)椭圆的右顶点为(2,0),设(2,0)关于直线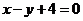 的对称点为
的对称点为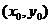
则 
所以 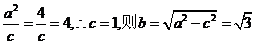

(2) 设 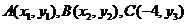
由 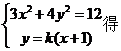 :
: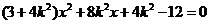
所以 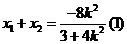
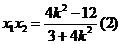
由 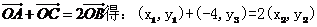
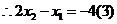
由(1)(3)得: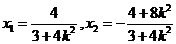 ,代入(2)得:
,代入(2)得:
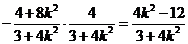 整理得:
整理得:
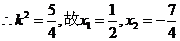
由于对称性,只需求出 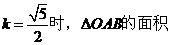 ,此时
,此时