江苏省海安高级中学高三数学第一次月考试卷
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合M={x| x = 2y, y∈R}, N = {x| x = y2, y∈R},则M∩N等于( )
A.{4,2} B.{(4,2)} C.N D.M
2.若函数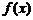 的图像与函数
的图像与函数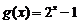 的图像关于点(0,1)对称,则
的图像关于点(0,1)对称,则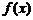 =( )
=( )
A.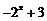 B.
B. 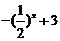 C.
C.
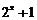 D.
D. 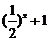
3.要使函数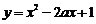 在[1, 2]上存在反函数,则a的取值范围是( )
在[1, 2]上存在反函数,则a的取值范围是( )
A.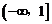 B.
B.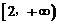 C.
C.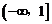
 D. [1,2]
D. [1,2]
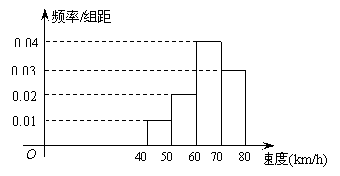
4.某公司在甲、乙、丙、丁四个地区分别有150 个、120个、180个、150个销售点. 公司
为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项
调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其收入和售后服务等
情况,记这项调查为②. 则完成①、②这两项调查宜采用的抽样方法依次是( )
A.分层抽样法,系统抽样法 B.分层抽样法,简单随机抽样法
C.系统抽样法,分层抽样法 D.简单随机抽样法,分层抽样法
5.已知函数y=log2x的反函数是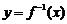 ,则函数
,则函数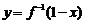 的图像是 ( )
的图像是 ( )
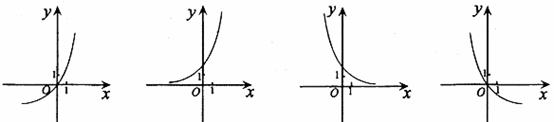
A B C D
 6.函数
6.函数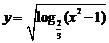 的定义域是( )
的定义域是( )
A.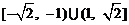
B. 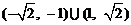
C . 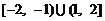
|
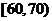 的汽车大约有( )
的汽车大约有( )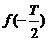 的值为 ( )
的值为 ( ) C.T D.-
C.T D.- <0的解集是
(
)
<0的解集是
(
)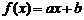
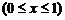 ,则“
,则“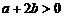 ”是“
”是“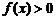 恒成立”的 ( )
恒成立”的 ( ) C. 充分必要条件
D. 既不充分又不必要条件
C. 充分必要条件
D. 既不充分又不必要条件
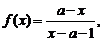 其反函数
其反函数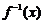 图像的对称中心是(-1,3),则a的值
图像的对称中心是(-1,3),则a的值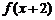 是偶函数,则
是偶函数,则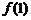 、
、 、
、 的
的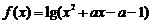 ,给出下列命题:①f (x)有最小值;②当a=0时,
,给出下列命题:①f (x)有最小值;②当a=0时,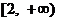 上有反函数;④若f (x)在区间
上有反函数;④若f (x)在区间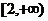 上是增函数,则实数a的取值范围是
上是增函数,则实数a的取值范围是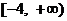 . 上述命题中正确的是
. 上述命题中正确的是
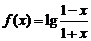 .
.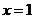 时有极值; ②图像过点(0, -3), 且在该点处的切线与直
时有极值; ②图像过点(0, -3), 且在该点处的切线与直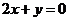 平行.
平行.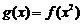 的单调递增区间.
的单调递增区间.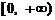 上是增函数.
上是增函数.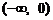 上也是增函数;
上也是增函数;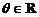 ,求实数m的取值范围,使不等式
,求实数m的取值范围,使不等式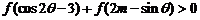 恒成立.
恒成立.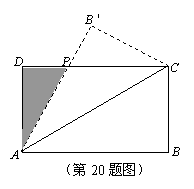 DC于点P. 设AB=x, 求△
DC于点P. 设AB=x, 求△ 的最大面积及相应的x值.
的最大面积及相应的x值.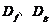 的函数,
的函数,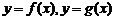 ,
,
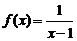 ,
,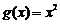 ,写出函数
,写出函数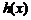 的解析式;
的解析式;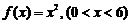 的图像,
的图像,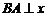 轴于A,曲线段OMB上一点
轴于A,曲线段OMB上一点 处的切线PQ交x轴于P,交线段AB于Q.
处的切线PQ交x轴于P,交线段AB于Q.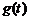 ,若函数
,若函数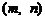 上单调递减,试求出m的最小值;
上单调递减,试求出m的最小值;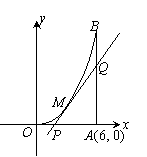 (3)
(3)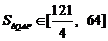 ,试求出点P横坐标的取值范围.
,试求出点P横坐标的取值范围. (15)200 (16)②③
(15)200 (16)②③  故函数的定义域是(-1,1). ………… 2分
故函数的定义域是(-1,1). ………… 2分 ,得
,得 (
( R),所以
R),所以 , …………… 5分
, …………… 5分
 (
( R).
………………… 7分
R).
………………… 7分
 =
= =-
=- ,所以
,所以 ,则
,则 .
………………… 1分
.
………………… 1分 即
即 解得
解得 ………………… 5分
………………… 5分 .
………………… 6分
.
………………… 6分 ,
, . …… 8分
. …… 8分











 ,且
,且 ,
, ,且
,且 .
………………… 2分
.
………………… 2分 在
在 上是增函数,∴
上是增函数,∴ .
………………… 4分
.
………………… 4分 ,
,
 , 即
, 即 上也是增函数.
……………… 6分
上也是增函数.
……………… 6分 上是增函数.
…………………… 7分
上是增函数.
…………………… 7分





 .
………… 10分
.
………… 10分 时,
时, 的最大值为
的最大值为 ,
, 时,不等式恒成立.
……………… 12分
时,不等式恒成立.
……………… 12分 ,于是
,于是 .
………………3分
.
………………3分 整理得
整理得 …………5分
…………5分 的面积
的面积  . ……7分
. ……7分 得
得 ………………8分
………………8分
 .
………………10分
.
………………10分 时,即当
时,即当
 时,S有最大值
时,S有最大值 ……11分
……11分 …………………5分
…………………5分 =x-1+
=x-1+ +2,
………………6分
+2,
………………6分
 ………2分
………2分 ………4分
………4分
 解得
解得  .
………6分
.
………6分 ………8分
………8分 在(0,4)上单调递增,
在(0,4)上单调递增,
 .
………14分
.
………14分