资阳市11月数学试题
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设全集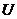 是实数集
是实数集 ,
,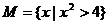 ,
,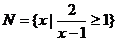 ,则图中阴影部分所表示的集合是 ( )
,则图中阴影部分所表示的集合是 ( )
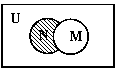 A.
A.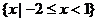 B.
B.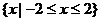
C. D.
D.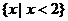
2. 已知tan160o=a,则sin2000o的值是 ( )
A. B.- C. D.-
3. 已知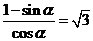 ,则
,则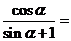 ( )
( )
A.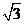 B.
B.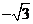 C.
C.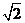 D.
D. 
4. 已知一动点P从(1,0)出发,沿圆 上逆时针旋转
上逆时针旋转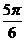 弧度到达Q点,则Q点的坐标是 ( )
弧度到达Q点,则Q点的坐标是 ( )
A.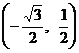 . B.
. B.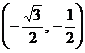 . C.
. C.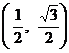 . D.
. D.
5. 如图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均等,那么两个指针同时落在奇数所在区域的概率是 ( )
 A.
A.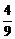 B.
B.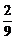 C.
C.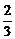 D.
D.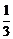
6. 将直线 绕点
绕点 顺时针旋转
顺时针旋转 ,再向上平移1个单位所得直线
,再向上平移1个单位所得直线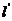 与圆
与圆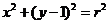 相切,则
相切,则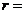 ( )
( )
A.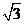 B.
B.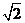 C.
C.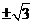 D.
D.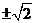
7. 无穷数列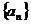 中,
中,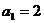 ,其前
,其前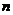 项和为
项和为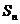 .当
.当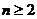 ,
, 时,
时,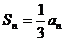 ,则
,则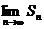 等于 ( )
等于 ( )
A.0
B.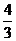 C.
C. D.3
D.3
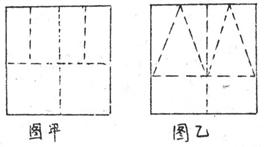 8. 将一边长为
8. 将一边长为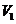 .若将同样的正方形纸片按照图乙中虚线所示的方法剪开后拼接为一正四棱锥,设其体积为
.若将同样的正方形纸片按照图乙中虚线所示的方法剪开后拼接为一正四棱锥,设其体积为 .则
.则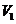 和
和 的大小关系
的大小关系
是 ( )
A.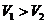 B.
B.
|
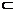 α,
α,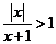 的解集为 ( )
的解集为 ( )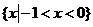 B.
B.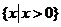
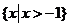 D.
D.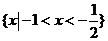
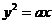 与其关于点(1,1)对称的曲线有两个不同的交点A、B,如果过这两个交点的直线的倾斜角是
与其关于点(1,1)对称的曲线有两个不同的交点A、B,如果过这两个交点的直线的倾斜角是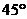 ,则实数a的值是 ( )
,则实数a的值是 ( )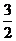 C.2
D.3
C.2
D.3 (
(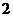 的正整数),如果在
的正整数),如果在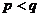 时有
时有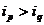 ,则称
,则称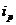 与
与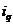 是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为此数组的“逆序数”. 例如,数组
是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为此数组的“逆序数”. 例如,数组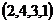 中有逆序“2,
中有逆序“2,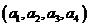 的“逆序数”是2,则
的“逆序数”是2,则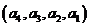 的“逆序数”是 ( )
的“逆序数”是 ( ) 的展开式中
的展开式中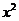 的系数为60,则实数
的系数为60,则实数 ________________.
________________.
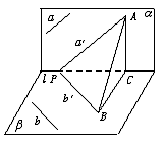
 14. 如图,在长方体
14. 如图,在长方体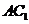 中,分别过BC和A1D1的两
中,分别过BC和A1D1的两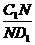 的值为 .
的值为 . 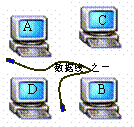 15. 如图,要用三根数据线将四台电脑A、B、C、D连接起来以实现资源共享,则不同的连接方案共有 种(用数字作答).
15. 如图,要用三根数据线将四台电脑A、B、C、D连接起来以实现资源共享,则不同的连接方案共有 种(用数字作答).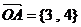 ,
,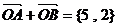 .
.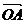 和
和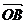 的夹角
的夹角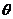 的大小(用反三角函数表示);
的大小(用反三角函数表示);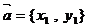 ,
,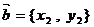 ,定义一种运算“
,定义一种运算“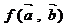 ”:
”: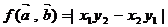 ,试计算
,试计算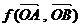 的值,并据此猜想
的值,并据此猜想 中,
中,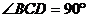 ,BC=CD=1,
,BC=CD=1,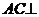 平面BCD,
平面BCD,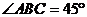 ,E是AB的中点.
,E是AB的中点.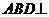 平面DEF.
平面DEF.
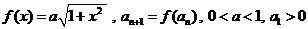 .
.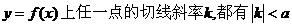 ;
;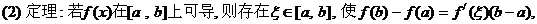 据此证明:
据此证明: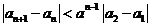 .
.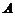 、
、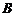 的距离为4,点
的距离为4,点 满足
满足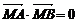 ,求点
,求点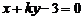 相切,试求实数
相切,试求实数 的值;
的值;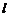 是经过椭圆
是经过椭圆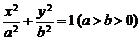 长轴顶点
长轴顶点 是两个焦点,点
是两个焦点,点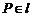 ,
,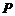 不与
不与 ,则有
,则有 ,类比此结论到双曲线
,类比此结论到双曲线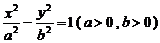 ,
,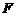 且与实轴垂直的直线,
且与实轴垂直的直线, 是两个顶点,点
是两个顶点,点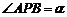 ,试求角
,试求角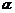 的取值范围.
的取值范围.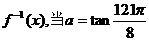 时,求证:
时,求证: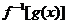
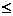 -1;
-1;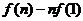 ,当
,当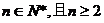 ,求函数h(a)的单调区间.
,求函数h(a)的单调区间. .
. 在
在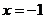 和
和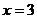 时取得极值,试求
时取得极值,试求 的值;
的值;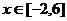 时,
时, . 14.2. 15.16. 16.13.
. 14.2. 15.16. 16.13. . 则 C=
. 则 C= (定值).
(定值).  ,
, ,
, .
. =
= =
=
 =
=
 =
= .
. .
. 时,△ABC面积S的最大值为
时,△ABC面积S的最大值为 .
.  ,
, ,
, ,
, ,∴
,∴  .
. 和
和 的夹角
的夹角 的大小为
的大小为 .
. .
. ,
, 的几何意义是以
的几何意义是以 、
、 为邻边的平行四边形的面积.
为邻边的平行四边形的面积. .
. ,
, ,
, .
. .
. .
.


 .
. ,故
,故 在
在 是增函数.
是增函数. 对于一切
对于一切 恒成立.
恒成立.


 的一般性知:
的一般性知: .
. 中点
中点 为原点,
为原点, 轴,建立平面直角坐标系,则
轴,建立平面直角坐标系,则 .
.
 ,由
,由 得
得 ,此即点
,此即点 的轨迹方程.
的轨迹方程. 向右平移一个单位,再向下平移一个单位后,得到圆
向右平移一个单位,再向下平移一个单位后,得到圆 ,
, .
. 在
在 的上方,并设
的上方,并设 ,则
,则 ,
, ,由于
,由于 且
且 ,
, .
. ,g(x)=
,g(x)= .
.
 是R上的减函数,
是R上的减函数,




 当
当 上是增函数.
上是增函数. 是减函数;
是减函数; 上是减函数.
上是减函数. 在
在 和
和 时取得极值,∴-1,3是方程
时取得极值,∴-1,3是方程 的两根,
的两根,
 ,当x变化时,有下表
,当x变化时,有下表 时f(x)的最大值为c+54.
时f(x)的最大值为c+54.