06-07冠龙高级中学高三质量调研数学试题 2006.10.8
本卷满分150分时间120分钟
一、填空题:(每小题5分,共计60分)
1.设集合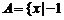 ≤x≤2},B={x|0≤x≤4},则A∩B=
.
≤x≤2},B={x|0≤x≤4},则A∩B=
.
2.函数y=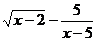 的定义域为________________.
的定义域为________________.
3.设函数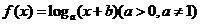 的图像过点
的图像过点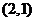 ,其反函数的图像过点
,其反函数的图像过点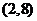 ,则
,则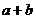 = .
= .
4.函数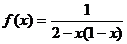 的最大值是 .
的最大值是 .
5.4名男生3名女生排成一排,若3名女生在一起,则不同的排法种数有 .(用数字作答)
6.方程 的解为 .
的解为 .
7.已知函数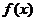 是奇函数,当
是奇函数,当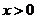 时, f(x)=x(1+x),则当
时, f(x)=x(1+x),则当 时,f(x)=
.
时,f(x)=
.
8.(文)在约束条件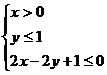 下,目标函数
下,目标函数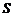 =
=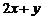 的最大值为
.
的最大值为
.
(理) 二项式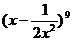 的展开式中的常数项是
.
的展开式中的常数项是
.
9.函数f(x)=ax
(a>0, a≠1)在[1, 2]中的最大值比最小值大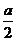 , 则a的值为 .
, 则a的值为 .
10.水箱中有水
11.在下列四个结论中,正确的有___ _____.(填序号)
①若A是B的必要不充分条件,则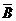 也是
也是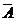 的必要不充分条件
的必要不充分条件
②“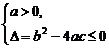 ”是“一元二次不等式ax2+bx+c≥0的解集为R”的充要条件
”是“一元二次不等式ax2+bx+c≥0的解集为R”的充要条件
③“x≠
④“x≠
二、选择题:(每小题4分,共计16分)
13.下列各组两个集合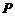 和
和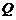 ,表示同一集合的是
( )
,表示同一集合的是
( )
A. 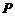 =
=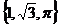 ,
,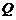 =
= B.
B. 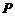 =
=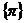 ,
,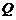 =
=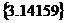
C. 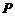 =
=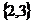 ,
,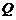 =
=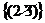 D.
D. 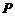 =
=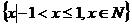 ,
,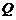 =
=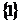
14.不等式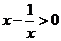 成立的充分不必要条件是
( )
成立的充分不必要条件是
( )
A.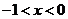 或
或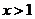 B.
B.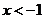 或
或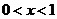 C.
C.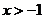 D.
D. 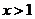
15.在一个口袋中装有5个白球和3个黑球,这些球除颜色外完全相同,从中摸出3个球,至少摸到2个黑球的概率等于 ( )
A.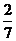 B.
B.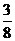 C.
C.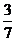 D.
D.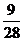
16.已知f(x)= ax (a>1), g(x)=bx (b>1), 当f(x1)= g(x2)=2时, 有x1>x2, 则a、b
的大小关系是 ( )
A a=b B a>b C a<b D 不能确定
三、解答题:(共计74分)
17.(本小题满分12分)设函数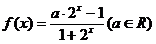 是R上的奇函数。
是R上的奇函数。
(1)求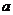 的值。
的值。
(2)求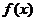 的反函数
的反函数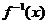 。
。
18.(本小题满分12分)已知命题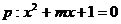 有两个不等的负根;命题
有两个不等的负根;命题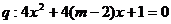 无实根.若命题p、q有且只有一个假命题,求实数m的取值范围.
无实根.若命题p、q有且只有一个假命题,求实数m的取值范围.
19.(本小题满分12分)讨论函数f(x)=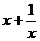 (x<0)的单调性,利用函数单调性的定义加以证明。
(x<0)的单调性,利用函数单调性的定义加以证明。
20.(本小题满分12分)已知集合A=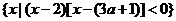 ,
,
B=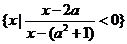 .
.
(1)当a=2时,求A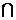 B; (2)求使B
B; (2)求使B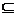 A的实数a的取值范围.
A的实数a的取值范围.
21.(本小题满分12分)根据市场调查,某商品在最近的40天内的价格f(t)与时间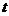 满足关系
满足关系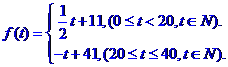 销售量g(t)与时间t满足关系
销售量g(t)与时间t满足关系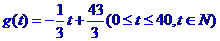
 求这种商品的日销售额(销售量与价格之积)的最大值
求这种商品的日销售额(销售量与价格之积)的最大值
22.(本小题满分14分)
函数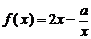 的定义域为
的定义域为 (
(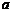 为实数).
为实数).
(1)当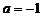 时,求函数
时,求函数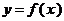 的值域;
的值域;
(2)若函数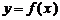 在定义域上是减函数,求
在定义域上是减函数,求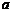 的取值范围;
的取值范围;
(3)讨论函数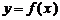 在
在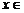
 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时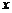 的值.
的值.
一、1. [0,2]
2. 2≤x<5或x>5
3. 4 4.  5. 720 6.
5. 720 6.  7. x(1-x)
7. x(1-x)
8.(文) 2 (理)  9. 10.
9. 10.  11. ①②④ 12. 0
11. ①②④ 12. 0
二、13. A 14. D 15. A 16.C
三、
17. 解:(1) 上的奇函数,
上的奇函数, 即
即 。
。
(2)由(1)得: ,即
,即 ,
,

 。
。
18. 解: 有两个不等的负根,
有两个不等的负根, …………3分
…………3分
 无实根,
无实根, 得
得 ……6分
……6分
有且只有一个为真,若p真q假,得 ………………9分
………………9分
若p假q真,得 ………………11分
………………11分
综合上述得 ……………………12分
……………………12分
19.f(x)在(-∞,-1)上是增函数, f(x)在(-1,0)上是减函数。 ………………4分
证明:任取x1,x2,使x1<x2<0,则
 ………………7分
………………7分
∵ x1<x2<0,x2-x1>0 x1?x2>0, 当x1<x2<-1时
∴ 
即 
∴ f(x)在(-∞,-1)上是增函数。 ………………10分
当-1<x1<x2<0时
f(x2)-f(x1)<0,即f(x2)<f(x1)
∴ f(x)在(-1,0)上是减函数。 ………………12分
20. 解:(1)当a=2时,A=(2,7),B=(4,5)∴ A B=(4,5).………4分
B=(4,5).………4分
(2)∵ B=( 时,A=(
时,A=(
要使B A,必须
A,必须 ,此时a=-1;…………………………………7分
,此时a=-1;…………………………………7分
当a= 时,A=
时,A= ,使B
,使B A的a不存在; ……………………………………8分
A的a不存在; ……………………………………8分
当a> 时,A=(2,
时,A=(2,
要使B A,必须
A,必须 ,此时1≤a≤3. ………………………………11分综上可知,使B
,此时1≤a≤3. ………………………………11分综上可知,使B A的实数a的取值范围为[1,3]∪{-1}………………………12分
A的实数a的取值范围为[1,3]∪{-1}………………………12分
21、解:解:据题意,商品的价格随时间 变化,且在不同的区间
变化,且在不同的区间 与
与 上,价格随时间
上,价格随时间 的变化的关系式也不同,故应分类讨论
的变化的关系式也不同,故应分类讨论
设日销售额为

⑴当 时,
时,

 。 ………………3分
。 ………………3分
所以,当 或11时,
或11时, 。
………6分
。
………6分
⑵当 时,
时,

 …9分
…9分
所以,当 时,
时, 。
…11分
。
…11分
综合(1)、(2)知当 或11时,日销售额最大,最大值为176。…………12分
或11时,日销售额最大,最大值为176。…………12分
22、解:(1)显然函数 的值域为
的值域为 ; ……………4分
; ……………4分
(2)若函数 在定义域上是减函数,
在定义域上是减函数,
则任取
 且
且 都有
都有 成立,
成立,
即 只要
只要 即可,
即可,
由
 ,故
,故 ,所以
,所以 ,
,
故 的取值范围是
的取值范围是 ; ……………9分
; ……………9分
(3)当 时,函数
时,函数 在
在 上单调增,无最小值,
上单调增,无最小值,
当 时取得最大值
时取得最大值 ;
;
由(2)得当 时,函数
时,函数 在
在 上单调减,无最大值,
上单调减,无最大值,
当 时取得最小值
时取得最小值 ;
;
当 时,函数
时,函数 在
在 上单调减,在
上单调减,在 上单调增,无最大值,
……………13分
上单调增,无最大值,
……………13分
当 时取得最小值
时取得最小值 . ……………14分
. ……………14分