-
网址:http://m.1010jiajiao.com/paper/timu/5160377.html[举报]
17.(14分)已知一个矩形由三个相同的小矩形拼凑而成(如图所示),用红、黄、蓝三种不同
颜色给3个小矩形涂色,每个小矩形只涂一种颜色(相邻两个小矩形可以用同一种颜色)。
(Ⅰ)试用树形图或表格列出所有可能着色结果;
(Ⅱ)求3个小矩形颜色都不相同的概率;
- 题目来源:08高考数学复习高一质量检测题 参考公式:锥体的体积公式,其中是锥体的底面积,是锥体的高. 如果事件互斥,那么. 用最小二乘法求线性回归方程系数公式.
参考答案
一、选择题:1-5:C D A B B 6-10: A C B B D
二、填空题:11.
65 12. ② ④ 13. 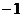 14.
14.
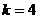

三、解答题:
15. 解:设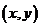 表示一个基本事件,则掷两次骰子包括:
表示一个基本事件,则掷两次骰子包括: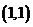 ,
,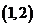 ,
,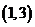 ,
,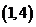 ,
, ,
,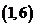 ,
,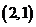 ,
,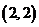 ,……,
,……,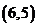 ,
,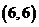 ,共36个基本事件.
,共36个基本事件.
(1)用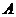 表示事件“
表示事件“ ”,则
”,则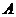 的结果有
的结果有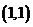 ,
,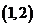 ,
,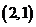 ,共3个基本事件.
,共3个基本事件.
∴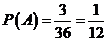 .
答:事件“
.
答:事件“ ”的概率为
”的概率为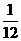 .
.
(2)用 表示事件“
表示事件“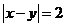 ”,则
”,则 的结果有
的结果有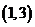 ,
,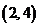 ,
,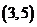 ,
,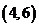 ,
,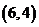 ,
,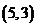 ,
, ,
,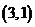 ,共8个基本事件.
∴
,共8个基本事件.
∴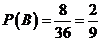 .
.
答:事件“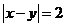 ”的概率为
”的概率为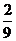 .
.
16.解:(1)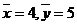 (2)由已知可得:
(2)由已知可得: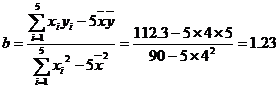
于是
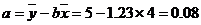 所以,回归直线方程是:
所以,回归直线方程是: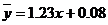 。
。
(3)由第(2)可得,当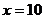 时,
时,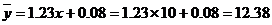 (万元)
(万元)
即估计使用10年时,维修费用是12.38万元。
17.(14分)(Ⅰ)(略)
(Ⅱ)记“3个矩形颜色都不同”为事件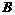 ,事件
,事件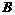 的基本事件有6个,故
的基本事件有6个,故
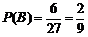 . ------11分
. ------11分
答:3个小矩形颜色都不同的概率为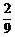 .
---- 12分.
.
---- 12分.
 18.(1)连结BE,由已知可得:
18.(1)连结BE,由已知可得:
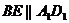 且
且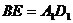
所以 四边形是平行四边形,
从而 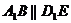 ,
,
又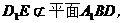

所以,当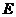 是
是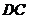 的中点时,有
的中点时,有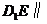 平面
平面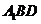 .
.
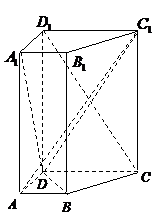 (2证明:在直四棱柱
(2证明:在直四棱柱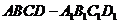 中,
中,
连结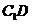 ,
, 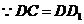 ,
,
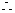 四边形
四边形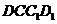 是正方形.
是正方形.
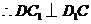 .又
.又 ,
, ,
,
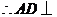 平面
平面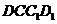 ,
, 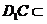 平面
平面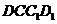 ,
,
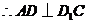 .
.
 平面
平面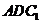 , 且
, 且 ,
,
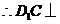 平面
平面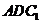 ,又
,又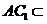 平面
平面 ,
,
 .
.
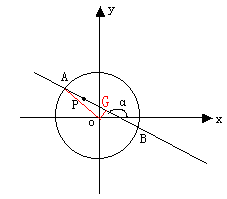
19.解:(1)过点O做OG⊥AB于G,连结OA,
当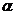 =1350时,直线AB的 斜率为-1,
=1350时,直线AB的 斜率为-1,
故直线AB的点斜式方程为: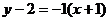
即  ,
,
∴OG=d=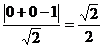 又∵r=
又∵r=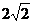
∴ ,∴
,∴ 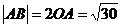
(2)设弦AB的中点为M(x,y),
当AB的斜率存在时,设为K,当AB不过原点时总有OM⊥AB,
则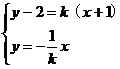 消去K,得
消去K,得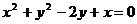 (*),易验证,原点满足(*)式;
(*),易验证,原点满足(*)式;
当直线AB的斜率K不存在时,中点M(-1,0)也满足(*)式,
故过点P的弦的中点的轨迹方程为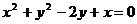
 所以
所以 的最小值为
的最小值为 ,最大值为
,最大值为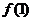 ………………3分
………………3分