-
1.某校有40个班,每班55人,每班选派3人参加“学代会”,在这个问题中样本容量是( )
A.40 B.50 C.120 D.150
-
2.将两个数a=5,b=9交换,使a=9,b=5,下面语句正确一组是 ( )
t = b
b = a
a = t
(A) (B) (C) D)a = c
c = b
b = a
a=b
b=a
b=a
a=b
3.函数s=0
i=2
Do
s=s+i
i= i+2
Loop until
Print s
End 第4题
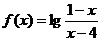 的定义域为(
)
的定义域为(
)
A.
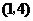 B.
B.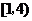
C.
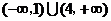 D.
D.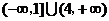
-
4.有下面的程序,运行该程序,要使输出的结果是30,
在处 应添加的条件是( )
A. i>12 B. i>10
 C. i=14 D.
i=10
C. i=14 D.
i=10 -
5.如果执行右面的程序框图,那么输出的
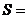 ( )
( )A.90 B.110
C.250 D.209
-
6.下图是NBA球员甲、乙在某个赛季参加的11场
比赛中
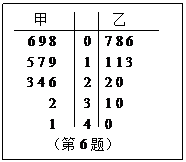 得分情况茎叶统计图,则他们得分的中位数
得分情况茎叶统计图,则他们得分的中位数分别为( )。
A.19、13
B.13、19
C.20、13
D.18、20(第5题)
-
7.某科研小组共有5个成员,其中男研究人员3人,女研究人员2名,现选举2名代表,至少有1名女研究人员当选的概率为( ) A.
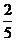 B.
B. 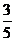 C.
C.  D.
以上都不对
D.
以上都不对 -
8.
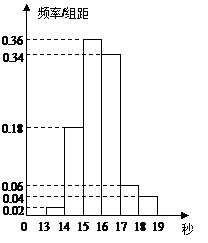 某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;
某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒; 第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为
第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为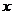 ,成绩大于等于15秒且小于17秒的学生人数为
,成绩大于等于15秒且小于17秒的学生人数为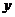 ,则从频率分布直方图中可分析出
,则从频率分布直方图中可分析出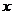 和
和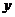 分别为(
)
分别为(
)A.0.9 45 B.0.9 35
C.0.1 35 D.0.1 45
-
9.直线
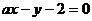 与圆
与圆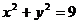 的位置关系是( )
的位置关系是( )A.相离 B.相交 C.相切 D.不能确定
-
10.计算机中常用的十六进制是逢16进1的记数制,采用数字0-9和字母A-F共16个
记数符号;这些符号与十进制的数的对应关系如下表:
十六进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
十进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例如,用十六进制表示:E+D=1B,则A×B=( )
A.B0 B。72 C。5F D。6E
-
11.
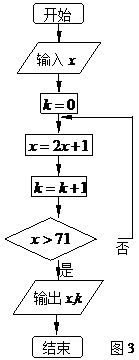 某校有学生2000人,其中高二学生630人,高三学生720人.为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本.则样本中高一学生的人数为___________.
某校有学生2000人,其中高二学生630人,高三学生720人.为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本.则样本中高一学生的人数为___________. -
12.某小组有3名男生和2名女生,从中任选出2名同学去参加演讲比赛,有下列4对事件:
①至少有1名男生和至少有1名女生,
②恰有1名男生和恰有2名男生,
③至少有1名男生和全是男生,
④至少有1名男生和全是女生,
其中为互斥事件的序号是: 。
-
13.已知定义域为R的函数
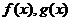 分别是奇函数、偶函数,
分别是奇函数、偶函数,若
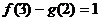 ,则
,则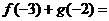 .
. -
14.按如右图3所示的程序框图运算.
若输入
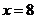 ,则输出
,则输出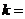 ;
;若输出
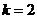 ,则输入
,则输入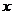 的取值范围是
.
的取值范围是
. (注:“
 ”也可写成“
”也可写成“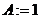 ”或“
”或“ ”,均表示
”,均表示赋值语句)
-
15.(12分) 将一枚质地均匀的正方形骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为
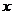 ,第二次出现的点数为
,第二次出现的点数为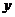 。
。(1)求事件“
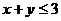 ”的概率;(2)求事件
”的概率;(2)求事件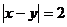 的概率。
的概率。 -
16.(12分)假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:
使用年限x
2
3
4
5
6
维修费用y
2.2
3.8
5.5
6.5
7.0
参考数据:
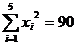 ,
,
若由资料知y对x呈线性相关关系。试求:
(1)求
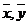 ; (2)线性回归方程
; (2)线性回归方程 ;
;(3)估计使用10年时,维修费用是多少?
-
17.(14分)已知一个矩形由三个相同的小矩形拼凑而成(如图所示),用红、黄、蓝三种不同
颜色给3个小矩形涂色,每个小矩形只涂一种颜色(相邻两个小矩形可以用同一种颜色)。
(Ⅰ)试用树形图或表格列出所有可能着色结果;
(Ⅱ)求3个小矩形颜色都不相同的概率;
-
18.
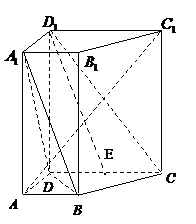 ( 14分)如图,在直四棱柱
( 14分)如图,在直四棱柱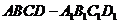 中,已知:
中,已知: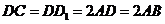 ,
,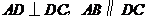 .
.(1)设
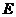 是
是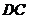 上中点,证明 :
上中点,证明 :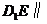 平面
平面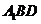 。
。(2)求证:
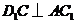 ;
; -
19.
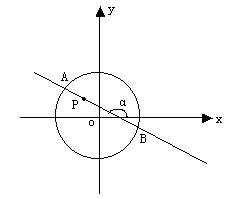 (14分) 如图,圆
(14分) 如图,圆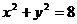 内有一点P(-1,2),
内有一点P(-1,2),AB为过点P且倾斜角为α的弦,
(1)当α=1350时,求
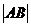 :(4分)
:(4分)(2)当弦AB被点P平分时,写出直线AB的方程。(5分)
(3)求过点P的弦的中点的轨迹方程。(5分)
-
20.(14分)已知函数
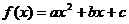 ,其中
,其中 。
。(1)若
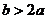 且函数
且函数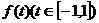 的最大值为2,最小值为
的最大值为2,最小值为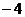 ,试求函数
,试求函数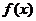 的最小值;
的最小值;(2)若对任意实数
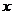 ,不等式
,不等式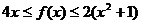 恒成立,且存在
恒成立,且存在 使
使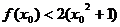 成立,求
成立,求 的值。
的值。
08高考数学复习高一质量检测题 参考公式:锥体的体积公式,其中是锥体的底面积,是锥体的高. 如果事件互斥,那么. 用最小二乘法求线性回归方程系数公式.参考答案
参考答案
一、选择题:1-5:C D A B B 6-10: A C B B D
二、填空题:11.
65 12. ② ④ 13. 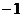 14.
14.
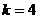

三、解答题:
15. 解:设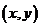 表示一个基本事件,则掷两次骰子包括:
表示一个基本事件,则掷两次骰子包括: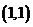 ,
,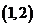 ,
,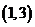 ,
,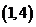 ,
, ,
,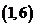 ,
,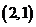 ,
,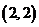 ,……,
,……,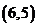 ,
,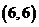 ,共36个基本事件.
,共36个基本事件.
(1)用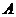 表示事件“
表示事件“ ”,则
”,则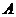 的结果有
的结果有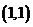 ,
,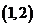 ,
,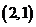 ,共3个基本事件.
,共3个基本事件.
∴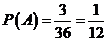 .
答:事件“
.
答:事件“ ”的概率为
”的概率为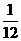 .
.
(2)用 表示事件“
表示事件“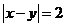 ”,则
”,则 的结果有
的结果有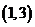 ,
,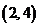 ,
,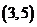 ,
,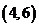 ,
,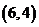 ,
,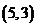 ,
, ,
,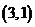 ,共8个基本事件.
∴
,共8个基本事件.
∴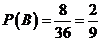 .
.
答:事件“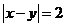 ”的概率为
”的概率为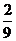 .
.
16.解:(1)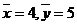 (2)由已知可得:
(2)由已知可得: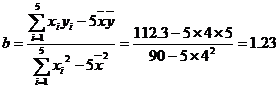
于是
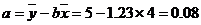 所以,回归直线方程是:
所以,回归直线方程是: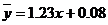 。
。
(3)由第(2)可得,当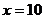 时,
时,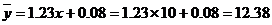 (万元)
(万元)
即估计使用10年时,维修费用是12.38万元。
17.(14分)(Ⅰ)(略)
(Ⅱ)记“3个矩形颜色都不同”为事件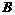 ,事件
,事件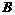 的基本事件有6个,故
的基本事件有6个,故
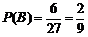 . ------11分
. ------11分
答:3个小矩形颜色都不同的概率为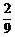 .
---- 12分.
.
---- 12分.
 18.(1)连结BE,由已知可得:
18.(1)连结BE,由已知可得:
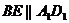 且
且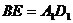
所以 四边形是平行四边形,
从而 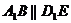 ,
,
又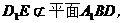

所以,当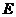 是
是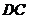 的中点时,有
的中点时,有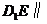 平面
平面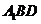 .
.
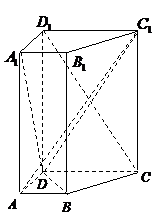 (2证明:在直四棱柱
(2证明:在直四棱柱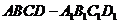 中,
中,
连结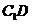 ,
, 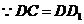 ,
,
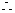 四边形
四边形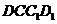 是正方形.
是正方形.
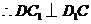 .又
.又 ,
, ,
,
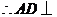 平面
平面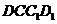 ,
, 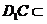 平面
平面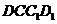 ,
,
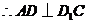 .
.
 平面
平面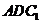 , 且
, 且 ,
,
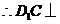 平面
平面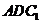 ,又
,又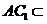 平面
平面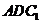 ,
,
 .
.
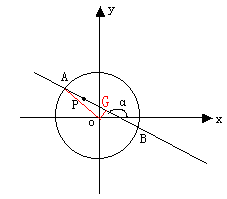
19.解:(1)过点O做OG⊥AB于G,连结OA,
当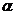 =1350时,直线AB的 斜率为-1,
=1350时,直线AB的 斜率为-1,
故直线AB的点斜式方程为: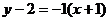
即  ,
,
∴OG=d=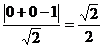 又∵r=
又∵r=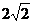
∴ ,∴
,∴ 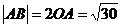
(2)设弦AB的中点为M(x,y),
当AB的斜率存在时,设为K,当AB不过原点时总有OM⊥AB,
则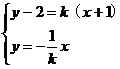 消去K,得
消去K,得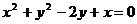 (*),易验证,原点满足(*)式;
(*),易验证,原点满足(*)式;
当直线AB的斜率K不存在时,中点M(-1,0)也满足(*)式,
故过点P的弦的中点的轨迹方程为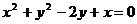
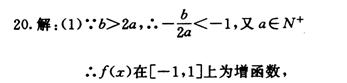
 所以
所以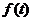 的最小值为
的最小值为 ,最大值为
,最大值为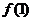 ………………3分
………………3分