-
网址:http://m.1010jiajiao.com/paper/timu/5159813.html[举报]
6.()已知函数f(x)是y=
 -1(x∈R)的反函数,函数g(x)的图象与函数y=-
-1(x∈R)的反函数,函数g(x)的图象与函数y=- 的图象关于y轴对称,设F(x)=f(x)+g(x).
的图象关于y轴对称,设F(x)=f(x)+g(x).(1)求函数F(x)的解析式及定义域;
(2)试问在函数F(x)的图象上是否存在两个不同的点A、B,使直线AB恰好与y轴垂直?若存在,求出A、B的坐标;若不存在,说明理由.
- 题目来源:08高考数学函数图象与图象变换测试 函数的图象与性质是高考考查的重点内容之一,它是研究和记忆函数性质的直观工具,利用它的直观性解题,可以起到化繁为简、化难为易的作用.因此,考生要掌握绘制函数图象的一般方法,掌握函数图象变化的一般规律,能利用函数的图象研究函数的性质. ●难点磁场 ()已知函数f(x)=ax3+bx2+cx+d的图象如图,求b的范围. ●案例探究 [例1]对函数y=f(x)定义域中任一个x的值均有f(x+a)=f(a-x),(1)求证y=f(x)的图象关于直线x=a对称;(2)
参考答案
难点磁场
解法一:观察f(x)的图象,可知函数f(x)的图象过原点,即f(0)=0,得d=0,又f(x)的图象过(1,0),∴f(x)=a+b+c①,又有f(-1)<0,即-a+b-c<0②,①+②得b<0,故b的范围是(-∞,0)
解法二:如图f(0)=0有三根,∴f(x)=ax3+bx2+cx+d=ax(x-1)(x-2)=ax3-3ax2+2ax,∴b=
-3a,∵a>0,∴b<0.
歼灭难点训练
一、1.解析:∵y=bax=(ba)x,∴这是以ba为底的指数函数.仔细观察题目中的直线方程可知:在选择支B中a>0,b>1,∴ba>1,C中a<0,b>1,∴0<ba<1,D中a<0,0<b<1,∴ba>1.故选择支B、C、D均与指数函数y=(ba)x的图象不符合.
答案:A
2.解析:由题意可知,当x=0时,y最大,所以排除A、C.又一开始跑步,所以直线随着x的增大而急剧下降.
答案:D

二、3.解析:g(x)=2log2(x+2)(x>-2)
F(x)=f(x)-g(x)=log2(x+1)-2log2(x+2)
=log2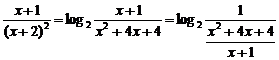
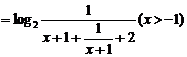
∵x+1>0,∴F(x)≤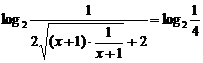 =-2
=-2
当且仅当x+1=  ,即x=0时取等号.
,即x=0时取等号.
∴F(x)max=F(0)=-2.
答案:-2
三、4.解:(1)S△ABC=S梯形AA′B′B+S梯形BB′C′C-S梯形AA′C′C.
(2)S=f(m)为减函数.
5.解:(1)依题意,设B(t, t),A(-t,
t),A(-t,  t)(t>0),C(x0,y0).
t)(t>0),C(x0,y0).
∵M是BC的中点.∴ =1,
=1, =m.
=m.
∴x0=2-t,y0=2m- t.在△ABC中,|AB|=2t,AB边上的高hAB=y0-
t.在△ABC中,|AB|=2t,AB边上的高hAB=y0- t=2m-3t.
t=2m-3t.
∴S=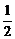 |AB|.hAB=
|AB|.hAB= 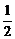 .2t.(2m-3t),即f(t)=-3t2+2mt,t∈(0,1).
.2t.(2m-3t),即f(t)=-3t2+2mt,t∈(0,1).
(2)∵S=-3t2+2mt=-3(t-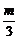 )2+
)2+ ,t∈(0,1
,t∈(0,1 ,若
,若 ,即
,即 <m≤3,当t=
<m≤3,当t=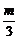 时,Smax=
时,Smax= ,相应的C点坐标是(2-
,相应的C点坐标是(2-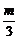 ,
,  m),若
m),若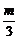 >1,即m>3.S=f(t)在区间(0,1]上是增函数,∴Smax=f(1)=2m-3,相应的C点坐标是(1,2m-3).
>1,即m>3.S=f(t)在区间(0,1]上是增函数,∴Smax=f(1)=2m-3,相应的C点坐标是(1,2m-3).
6.解:(1)y= -1的反函数为f(x)=lg
-1的反函数为f(x)=lg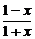 (-1<x<1
(-1<x<1 .
.
由已知得g(x)= ,∴F(x)=lg
,∴F(x)=lg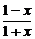 +
+ ,定义域为(-1,1).
,定义域为(-1,1).
(2)用定义可证明函数u=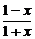 =-1+
=-1+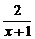 是(-1,1)上的减函数,且y=lgu是增函数.∴f(x)是(-1,1)上的减函数,故不存在符合条件的点A、B.
是(-1,1)上的减函数,且y=lgu是增函数.∴f(x)是(-1,1)上的减函数,故不存在符合条件的点A、B.
7.解:(1)y=f(x)=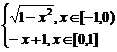 .图略.
.图略.
y=f(x)的曲线绕x轴旋转一周所得几何体的表面积为(2+ )π.
)π.
(2)当f1(x+a)=f2(x)有两个不等实根时,a的取值范围为2- <a≤1.
<a≤1.
(3)若f1(x)>f2(x-b)的解集为[-1,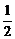 ],则可解得b=
],则可解得b=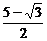 .
.
8.(1)g(x)=x-2+ .(2)b=4时,交点为(5,4);b=0时,交点为(3,0).
.(2)b=4时,交点为(5,4);b=0时,交点为(3,0).
(3)不等式的解集为{x|4<x< 或x>6
或x>6 .
.