-
网址:http://m.1010jiajiao.com/paper/timu/5159628.html[举报]
2.若
 的终边所在象限是 (
)
的终边所在象限是 (
)A.第一象限 B.第二象限 C.第三象限 D.第四象限
- 题目来源:专题四 高考数学三角函数复习训练 高考试题中的三角函数题相对比较传统,位置靠前,通常以简单题形式出现。因此,在复习过程中要特别注重三角知识的基础性,突出三角函数的图象及其变换、周期性、单调性、奇偶性、对称性等性质,以及化简、求值和最值等重点内容的复习,要求考生熟练记忆和应用三角公式及其恒等变形,同时要注重三角知识的工具性.近年来,三角函数与向量联系问题有所增加,三角知识在几何及实际问题中的应用也是考查重点,应给于充分的重视。
参考答案:
一.选择题:
1.C. 2.D. 3.B 4.D. 5.A 6.A. 7.D. 8.A 9. A 10.A 11。D 12.D
9. [解析]:要使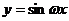 (ω>0)在区间[0,1]至少出现2次最大值
(ω>0)在区间[0,1]至少出现2次最大值
只需要最小正周期

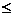 1,故
1,故
 10.
10. [解析]:∵ cosB=
[解析]:∵ cosB= ,∴B是钝角,∴C就是锐角,即cosC>0,故选A
,∴B是钝角,∴C就是锐角,即cosC>0,故选A
二.填空题:
13.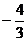 或
或
[解析]: ∵ -
-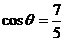 >1,且
>1,且 ∈(0,π)∴
∈(0,π)∴ ∈(
∈(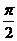 ,π)
,π)
∴
( -
- ∴2sin
∴2sin cos
cos =
=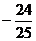
∴ +
+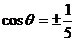
∴sin =
= cos
cos =
= 或sin
或sin =
= cos
cos =
=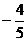
tan =
=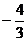 或
或
14.
[解析]: ∵
 =
=
∴
 =
=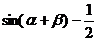
∴

又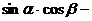
 =
=
∴
 =
=
∴

故
15.②④
[解析]:∵若-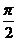 <
< <
< <
<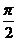 ,则
,则 范围为(-π,0)∴①错
范围为(-π,0)∴①错
∵若 =
= ,
,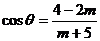 ,则m∈(3,9)
,则m∈(3,9)
又由 得m=0或 m=8
得m=0或 m=8
∴m=8
故③错
16.①②④.
三、解答题:
17.解: 原式


 =
=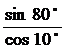 =
=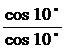 =1
=1
18.解:由题设知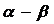 为第一象限角
为第一象限角
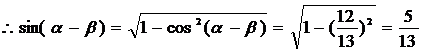
由题设知 为第三象限角
为第三象限角
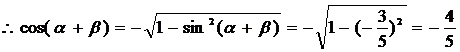

19.(Ⅰ)解: .
.
因此,函数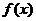 的最小正周期为
的最小正周期为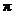 .
.
(Ⅱ)解法一:因为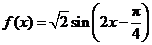 在区间
在区间 上为增函数,在区间
上为增函数,在区间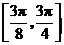 上为减函数,又
上为减函数,又 ,
,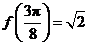 ,
, ,
,
故函数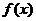 在区间
在区间 上的最大值为
上的最大值为 ,最小值为
,最小值为 .
.
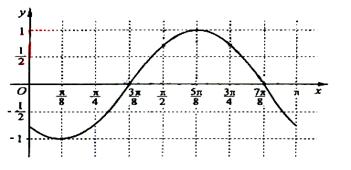
解法二:作函数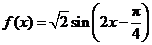 在长度为一个周期的区间
在长度为一个周期的区间 上的图象如下:
上的图象如下:

由图象得函数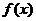 在区间
在区间 上的最大值为
上的最大值为 ,最小值为
,最小值为 .
.
20.本小题主要考查三角函数性质及图像的基本知识,考查推理和运算能力,满分12分.
解:(Ⅰ) 的图像的对称轴,
的图像的对称轴,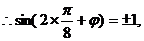


(Ⅱ)由(Ⅰ)知
由题意得
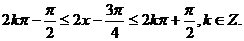
所以函数
(Ⅲ)由
|
x |
0 |
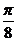 |
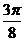 |
 |
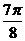 |
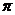 |
|
y |
 |
-1 |
0 |
1 |
0 |
 |
|

20 . 解:如图,延长AB交直角走廊于A1、B1,设∠CDE1=,则∠B1A1E1=,∈(0,).
∵ CD=AB=A1B1-AA1-BB1,
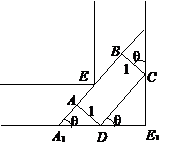 而 A1B1=1.5(+),AA1=cot,BB1=tan,
而 A1B1=1.5(+),AA1=cot,BB1=tan,
∴ CD=1.5(+)―cot―tan
=.
令sin+cos=t,则t∈(1,].
令 f(t)== ,
显然,函数f(t)在(1,]上是减函数,所以当t=,即=时,
CDmin=f(t)min=3-2.
故平板车的长度不能超过3-2米.
19.解:(Ⅰ)
 .
.
∵ 角 A
为锐角,∴
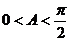 ,
, .
.
∴ 当 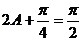 时,
时,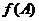 取得最大值,其最大值为
取得最大值,其最大值为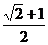 .
.
(Ⅱ)由 得
得  ,∴
,∴ .
.
∴  ,
,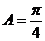 .又 ∵
.又 ∵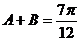 ,∴
,∴  .∴
.∴  .
.
在 △ABC
中,由正弦定理得: .∴
.∴ 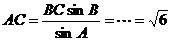 .
.
21.解:(1)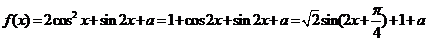
则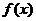 的最小正周期
的最小正周期 ,
,
且当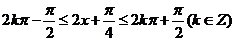 时
时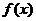 单调递增.
单调递增.
即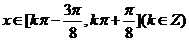 为
为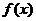 的单调递增区间(写成开区间不扣分).
的单调递增区间(写成开区间不扣分).
(2)当 时
时 ,当
,当 ,即
,即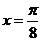 时
时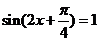 .
.
所以 .
.
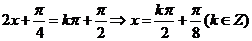 为
为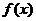 的对称轴.
的对称轴.
22. (1)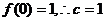




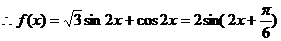
(2)由题意,知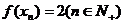
即

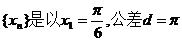 的等差数列
的等差数列
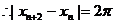

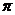
23.已知函数 的图象上以N(1,n)为切点的切线倾斜角为
的图象上以N(1,n)为切点的切线倾斜角为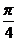 .
.
(1)求m,n的值;
(2)是否存在最小的正整数k,使得不等式 恒成立?若存在,求出最小的正整数k,否则请说明理由.
恒成立?若存在,求出最小的正整数k,否则请说明理由.
(3)求出 的取值范围.
的取值范围.
22.(1)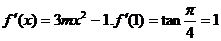


从而由
 ……………………4分
……………………4分
(2)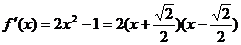
令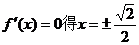 …………………………5分
…………………………5分
在[-1,3]中,当 为增函数,
为增函数,
当 为减函数
为减函数
 时取得极大值
时取得极大值
当 为增函数时f(3)
为
为增函数时f(3)
为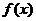 的极大值………………8分
的极大值………………8分
比较 ………………9分
………………9分

 ……………………10分
……………………10分
(3)
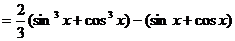
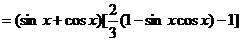
=
=
=
 …………………………14分
…………………………14分
五、复习的建议
立足课本,抓好基础。注意三角函数作为函数的特征的运用。如在解决周期性、奇偶性、最值等问题时有关数学思想的运用。
1, 加强对三角函数图象的研究。使学生熟练地求解有关图象的特征、图象的对称性、变换、解析式、五点作图等问题。
2, 熟练掌握三角变换的基本公式,弄清公式的推导关系和互相联系,把基本公式记准用熟。在三角变换中经常出现公式的逆用或变形,尤其是二倍角余弦公式、两角和差的正切的变形应用较为广泛。另外,辅助角公式应用也较多,也是考生常出错的地方,应引起注意。
3, 提高学生解决常见综合题的能力,提高运用所学知识分析、提取解题信息的能力。
4, 提高学生的运算和表达的能力,以及确定运算方向和实现转化的能力。
6,三角形中的三角函数问题,要注意正弦定理、余弦定理是实现“边角互换”的关键,而三角变换是解决问题的重要手段。解三角形涉及的变换较多,综合性强,对考生的应变能力和计算能力要求较高,一定要注意控制难度。