-
网址:http://m.1010jiajiao.com/paper/timu/5159066.html[举报]
2. 已知点
 在第三象限, 则角
在第三象限, 则角 的终边在( ).
的终边在( ).A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
- 题目来源:08届高考文科数学六校第二次联考 数 学(文科)科试卷 本卷分第Ⅰ卷(选择题、填空题)和第Ⅱ卷解答题两部分,满分150分.考试用时间120分钟. 参考公式: 锥体的体积公式, 其中是锥体的底面积, 是锥体的高. 第Ⅰ卷(选择题、填空题共70分)
文科数学答案
一、选择题
BBAAA BAADD
二、填空题
11. 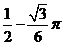 12.
2 13.
12.
2 13. 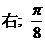 14.
14.

三、解答题(共6小题,满分80分)
15. 解:(Ⅰ) ,
, 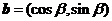 ,
,
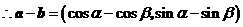 . ………………………………1分
. ………………………………1分
 ,
,  ,
………………………………3分
,
………………………………3分
即
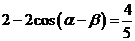 ,
,  .
……………………………6分
.
……………………………6分
(Ⅱ)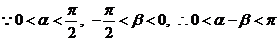 , ………………………7分
, ………………………7分
 ,
, 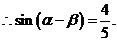 …………………………………9分
…………………………………9分
 ,
,  , ……………………………………10分
, ……………………………………10分 
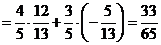 . …………………………………………………………12分
. …………………………………………………………12分
16. 解: 若 , 则
, 则 ,
, 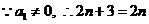 , 不合要求; ………3分
, 不合要求; ………3分
若 , 则
, 则 , ……………………6分
, ……………………6分
 ,
………………………………………9分
,
………………………………………9分
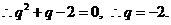 综上,
综上, 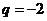 . ……………………12分
. ……………………12分
17. 证明:(1)取PD中点Q, 连EQ
, AQ , 则 ……………………………………1分
……………………………………1分

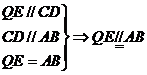 …………………………………………2分
…………………………………………2分
 ………………3分
………………3分
 ………………………5分
………………………5分
 (2)
(2) 
 . ………………………………………10分
. ………………………………………10分
解:(3) …………………………………11分
…………………………………11分
 . ………………………………14分
. ………………………………14分
18. 解:(1) 因为 , ………………………2分
, ………………………2分
而 , 故
, 故 ,
………………………3分
,
………………………3分
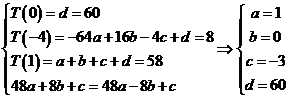 . …………………6分
. …………………6分
∴ .
…………………………………7分
.
…………………………………7分
(2)  , 由
, 由  ……………………9分
……………………9分
当 在
在 上变化时,
上变化时, 的变化情况如下表:
的变化情况如下表:
 |
-2 |
(-2,-1) |
-1 |
(-1,1) |
1 |
(1,2) |
2 |
 |
|
+ |
0 |
- |
0 |
+ |
|
 |
58 |
增函数 |
极大值62 |
减函数 |
极小值58 |
增函数 |
62 |
…………………………………12分
由上表知当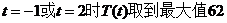 ,说明在上午11:00与下午14:00,该物体温度最高,最高温度是62℃.
…………………14分
,说明在上午11:00与下午14:00,该物体温度最高,最高温度是62℃.
…………………14分
19. 解: (1) 假设函数 属于集合
属于集合 , 则存在非零常数
, 则存在非零常数 , 对任意
, 对任意 , 有
, 有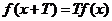 成立, ……………………………………………3分
成立, ……………………………………………3分
即:  成立. 令
成立. 令 , 则
, 则 , 与题矛盾. 故
, 与题矛盾. 故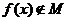 .
………………………………6分
.
………………………………6分
(2)  , 且
, 且 , 则对任意
, 则对任意 , 有
, 有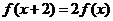 ,
……………8分
,
……………8分
设 , 则
, 则 ,
,  ………………11分
………………11分
当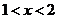 时,
时, 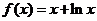 ,
,
故当 时,
时, 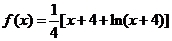 . ……………………………14分
. ……………………………14分
20. 解: (1) 由题知: 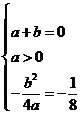 , 解得
, 解得 ,
故
,
故 . …………3分
. …………3分
(2) 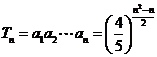 ,
………………………………………………5分
,
………………………………………………5分
 ,
,
 , …………………………………7分
, …………………………………7分
又 满足上式. 所以
满足上式. 所以 . …………………8分
. …………………8分
(3) 若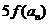 是
是 与
与 的等差中项, 则
的等差中项, 则 , ………………………9分
, ………………………9分
从而 , 得
, 得 .
…………10分
.
…………10分
因为 是
是 的减函数, 所以
的减函数, 所以
当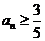 , 即
, 即 时,
时,  随
随 的增大而减小, 此时最小值为
的增大而减小, 此时最小值为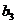 ;
;
当 , 即
, 即 时,
时,  随
随 的增大而增大, 此时最小值为
的增大而增大, 此时最小值为 .
…………12分
.
…………12分
又 , 所以
, 所以 ,
,
即数列 中
中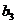 最小, 且
最小, 且 . …………14分
. …………14分